今までは特徴量多ければ良いと思ってたけど、色々調べてたらどうやら違うみたい。
確かに、多ければ一概にいいってものでもなさそうだね。
ボストンの住宅価格の予測を、重回帰で行いましたが、いろいろ調べていると、データの選択をおこなっていないと、楽観的な予測を行っていたり、問題が発生している可能性があることがわかりました。そんな感じで、特徴量の選択ついて調べました。
ボストンの住宅価格の予測、重回帰についてはこちらの記事もご参考ください。

こんな人の役にたつかも
・機械学習プログラミングを勉強している人
・教師あり学習、回帰の勉強をしている人
・回帰問題の特徴量選択について知りたい人
相関係数について整理
だんだん機械学習プログラミングを勉強していたのが、統計学とか数学的な勉強になってきた気がしているこの頃です。それだけ色々な分野に支えられて成り立っているということですね^^;
そして、唐突に「相関係数」という言葉を出します・・・
相関係数って、昔聞いたことあるような・・・
相関係数
相関係数は、ある変数(Xとします)がともう一方の変数(Yとします)が「正の相関」を持っている時、+1に近づきます。
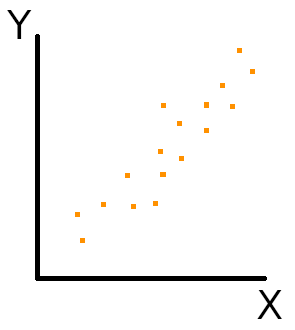
「正の相関」は、ある変数Xが増加するともう一方の変数Yも増加するという関係がみられるものです。
次に、ある変数Xともう一方の変数Yが「負の相関」を持っている時、−1に近づきます。
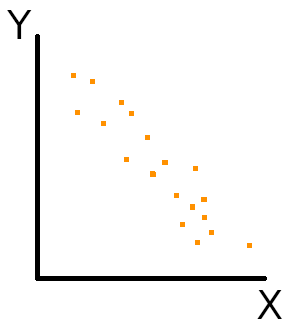
「負の相関」は、ある変数Xが増加するともう一方の変数Yは減少するという関係がみられるものです。
また、0に近いと上のような関係性がみられないということになります。
相関係数については、wikipediaのイメージの部分を参考にすると直感的にわかると思います。
まずは、+1や−1に近いほど関係性が強いって捉え方でいいんだね。
ここではそんな感じだね。
特徴量選択をする
相関係数がわかったところで、ボストンの住宅価格データの特徴量について相関係数を算出していきます。
目的変数「MEDV(住宅価格データ)」に対して、先ほどの相関係数のような関係性がシンプルにみられるものであれば、とても簡単に関係性が見出せますよね。そのような特徴量があれば使わない手はない!ということらしいですね。
シンプルイズベスト
相関関係を確認しよう!
ということで、ボストンの住宅価格データの目的変数「MEDV」に対して相関係数が+1や−1に近いものを探してみたいと思います。
説明変数が多ければ良いという訳ではなく、目的変数と相関関係が強い説明変数を入れると良いとのことでした。
from sklearn.datasets import load_boston
import pandas as pd
import seaborn as sns
panda_box = load_boston()
#住宅価格データをpandasのデータフレーム型に
boston = pd.DataFrame(panda_box.data, columns=panda_box.feature_names)
#目的変数「MEDV」も列として表に加える。
boston['MEDV'] = panda_box.target
#seaboneで全ての組み合わせの相関係数を計算して表示
sns.set(rc={'figure.figsize':(11.7,8.27)})
correlation_matrix = boston.corr().round(2)
sns.heatmap(data=correlation_matrix, annot=True)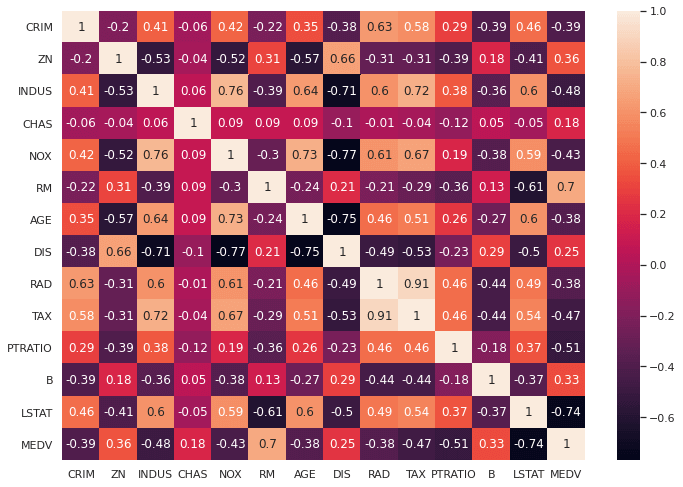
とても綺麗な絨毯みたいな表ができた。
この表は、住宅価格データMEDVを含む全ての特徴量の組み合わせで相関係数を計算したものになります。
そして今回、MEDVと相関が強そうなものを探します。

「RM」(部屋数)が0.7と、正の相関を、「LSTAT」が-0.74という負の相関を示しています。
よって、ボストンの住宅価格データ「MEDV」を回帰するための特徴量として「RM」と「LSTAT」は採用されることとなります。
だいたい0.7より大きいかどうかが目安かな?
「RM」と「LSTAT」のみで回帰をしてみよう
#最小二乗法による重回帰(共線性を考慮して特徴量を選択)
from sklearn.datasets import load_boston
from sklearn import linear_model
from sklearn.model_selection import train_test_split
panda_box = load_boston()
X = panda_box.data
#0:CRIM 1:ZN 2:INDUS 3:CHAS 4:NOX 5:RM 6:AGE 7:DIS 8:RAD 9:TAX 10:PTRATIO 11:B 12:LSTAT
#「RM」と「LSTAT」の列のみ選択
X = X[:,[10, 12]]
y = panda_box.target
#訓練データとテストデータに分割(テストデータ25%)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25)
#線形回帰を作成して訓練させる
reg = linear_model.LinearRegression().fit(X_train,y_train)
print("テストデータで評価")
print("決定係数R: {:.3f}" .format(reg.score(X_test, y_test)))テストデータで評価
決定係数R: 0.536「RM」のみの単回帰の時は0.4程度の決定係数だったので、単回帰の時より精度が上昇している感じです。
重回帰の0.7程度の精度と比較すると特徴量を多くした方がいいかな、という感じもします。ただ、考えなく全ての特徴量を取り入れると、「多重共線性」という問題が発生している可能性があるらしく、0.7という重回帰の精度は楽観的な見積もりとなっているかもしれません。次回は、「多重共線性」の側面からも特徴量選択を行いたいと思います。
単回帰の記事はこちらをご参考ください。

今回、大いに参考になったサイトです。ボストン住宅データの回帰について基本的なデータ選択の流れから一通り説明してある情報です。(英語のサイトですが、興味ある方は読んでみてください。)


