【AIプログラミング】ボストン住宅価格データで重回帰をしてみる

線形モデルは、１特徴量での予測だと、直線を引くだけなので、あまり良い予測ができなさそうな雰囲気がありました。特に、サンプルデータ数より特徴量が多いときには、効果が得られる可能性あるらしいです。今回は、ボストンの住宅価格データを利用して、「部屋数」のみを利用するのではなく、そのほかの特徴量も利用した重回帰をやってみたいと思います。

ボストンの住宅価格データの単回帰についてはこちらの記事をご参考ください。

こんな人の役に立つかも

・機械学習プログラミングを勉強している人

・ボストンの住宅価格データの回帰プログラムを勉強している人

・重回帰について知りたい人

重回帰をプログラミングしてみる

重回帰では、次のような式をデータに合わせていきます。

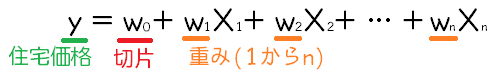
今回は13の特徴量が住宅価格を決めるような回帰モデルを作成したいです。

scikit-learnのLinearRegressionで訓練(fit)することで、実データから、w1～w13までと、w0切片を求めることができます。

また、未知のデータへの当てはまりを求めたいので、あらかじめtrain_test_splitによって25%分のテストデータを作成しておきます。

プログラミング

importから、ボストン住宅価格データを読み込みます。久しぶりのtrain_test_splitです。

#最小二乗法による重回帰
from sklearn.datasets import load_boston
from sklearn import linear_model

from sklearn.model_selection import train_test_split

panda_box = load_boston()

X = panda_box.data
y = panda_box.target

#訓練データとテストデータに分割(テストデータ25%)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25)

scikit-learnのLinearRegressionを読み込んで、訓練させます。今回は全データの75%を訓練データとしています。

#線形回帰を作成して訓練させる
reg = linear_model.LinearRegression().fit(X_train,y_train)
#決定係数を求める
print(reg.score(X_test, y_test))

scoreの結果は次のようになりました。

※データの内容によるため、train_test_splitの実行毎に結果は変化します。

0.6628069000866117

決定係数は、統計学の用語で、予測した線（や平面や超平面）がどれくらい当てはまりが良いかとい尺度になる数値とのことです。wikipediaの最初の二行で雰囲気がつかめました！1.0に近いほど、良いモデルができているということですね。

ということで、scoreをすることで、

「訓練した回帰モデルがどれくらい未知のデータ予測に当てはまっていたか」

を示す数値ということになるんですね。

※「決定係数R」は英語で「coefficient of determination R^2」というみたいですね。メモです。

最後に、切片と重みを確認してみます。

#切片と重みを確認
print("重み")
print(reg.coef_)
print("切片")
print(reg.intercept_)

重み
[-1.06844210e-01  3.27909295e-02  2.20528546e-02  4.30059968e+00
 -1.43752650e+01  4.22226227e+00  2.35105744e-03 -1.24097749e+00
  2.89165110e-01 -1.29828627e-02 -8.46921794e-01  7.01899198e-03
 -5.05107330e-01]
切片
30.242155786583524

13の特徴量の重みと、切片が計算されました。

単回帰との比較

特徴量「RM」のみの、単回帰も次のようにscoreを使って評価してみました。

#単回帰によるscore
from sklearn.datasets import load_boston
from sklearn import linear_model

from sklearn.model_selection import train_test_split

panda_box = load_boston()

#特徴量「RM」のみにする
X = panda_box.data[:,5]
y = panda_box.target

#訓練データとテストデータに分割(テストデータ25%)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25)

#1次元配列から2次元配列の表形式に変換
X_train = X_train.reshape(-1,1)
X_test = X_test.reshape(-1,1)

#線形回帰を作成して訓練させる
reg = linear_model.LinearRegression().fit(X_train,y_train)

print(reg.score(X_test, y_test))
#切片と重みを確認
print("重み")
print(reg.coef_)
print("切片")
print(reg.intercept_)

0.4374673367271549
重み
[9.19849801]
切片
-35.067616027269985

ボストン住宅価格データの単回帰と重回帰の比較

train_test_splitの分け方で決定係数が0.4～0.5くらいまで幅があるのですが、何回か実行した結果、0.7になることはなかったので、単回帰の性能は大体これくらいかと考えられます。

一方、重回帰によるモデル作成では、何回か実行したところ0.5～0.7くらいの精度がでていました。

今回は、特徴量を増やすことで、未知データに対してより精度の高い回帰モデルができたといってよいと思います。