【AIプログラミング】線形回帰でボストン住宅価格の予測、単回帰でやってみる

前回までで、scikit-learnで読み込むことができるボストンの住宅価格データについてみてきました。このデータを利用して、一番簡単な回帰アルゴリズムの「線形モデルのLinearRgression」を使って、単回帰を行ってみました。単回帰を行うことで、機械学習の教師あり学習「回帰」のイメージがよりつかめると思います。

ボストン住宅価格データの記事は、こちらをご参考ください。

用語の整理から

線形モデルと単回帰

次のような式を思い浮かべます。

y = aX + b

このような直線の式で「データ変化を予測する線」を表現するようなものを「線形モデル」といいます。

上の式のように、Xの変化によってyが決定するとき、ただ一つのXという説明変数でｙという目的変数が決定するので、単回帰といいます。

前回の散布図の確認で、今回はあえて住宅価格に関連性がありそうな「RM、部屋数」を説明変数として選択しました。そのため、今回は「RM（部屋数）」に対する「MEDV（住宅価格）」の関係性を線形モデルで求めるということです。

線形モデルについては以前の記事にも書いていますので、ご参考ください。

最小二乗法

線形モデルは、今あるデータをもとに「一番当てはまりの良い予測直線」を作成していきます。そのためには、具体的に今あるデータから、先ほどの「y = aX + b」の「a」と「b」を求める必要があります。

その手法の一つが「最小二乗法」と呼ばれるものです。

この最小二乗法という手法は、scikit-learnのLinearRegressionというプログラムで簡単に利用することができます。

最小二乗法で予測線を引いてみる

import~データの読み込み

まずはボストン住宅価格のデータと、線形回帰（最小二乗法による線形モデルLinearRegression）を読み込みます。あとあと、pandasやnumpyも使いそうだったので、読み込んでいます。また、グラフを描くmatplotlibも読み込んでおきます。

最後に、ボストン住宅価格データをpanda_boxという変数に入れています。

#最小二乗法による単回帰
from sklearn.datasets import load_boston
from sklearn import linear_model

import matplotlib.pyplot as plt

import pandas as pd
import numpy as np

panda_box = load_boston()

訓練用データの作成

ボストンの住宅価格データの特徴量を数値で選択できるような仕組みにしてあります。今回は、「部屋数RM」をただ一つの特徴量とするため、select_xという変数に5をいれて設定できるようにしています。

#単回帰用に特徴量を１種類に絞る
#0:CRIM 1:ZN 2:INDUS 3:CHAS 4:NOX 5:RM 6:AGE 7:DIS 8:RAD 9:TAX 10:PTRATIO 11:B 12:LSTAT
select_x = 5
X = panda_box.data[:,select_x]
_df = X
#print(X)
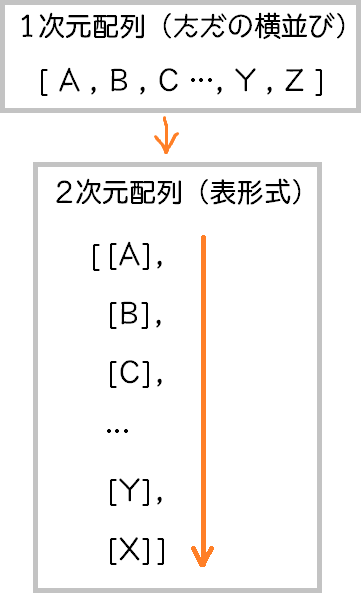
#1次元配列から2次元配列に変換
X = X.reshape(-1,1)
#print(X)
y = panda_box.target
target_df = y
y = y.reshape(-1,1)

Xを「reshape(-1,1)」としているのは、元のデータが1次元配列（横並びのデータ）なので、scikit-learnの訓練できるデータ形式の２次元配列（表形式のデータ）に変換するためです。このreshape(-1,1)はいろいろと便利に使えるみたいで、覚えておきます。

訓練の時は、特徴量が２個以上ある場合もあるので、２次元配列の形で受け取るんですね。

分類のときと同じように、機械学習アルゴリズムを作成して、fitで訓練できます。

#線形モデルを作成して最小二乗法で訓練
reg = linear_model.LinearRegression()
reg.fit(X,y)

#直線の傾き（重み）
print(reg.coef_)
#切片
print(reg.intercept_)

今回は、１特徴量なので、y = aX + bのa、傾きが「coef_」に、bの切片「intercept_」に入ってきます。今回は、↓のような結果になりました。

[[9.10210898]]
[-34.67062078]

今回のデータに当てはめると、「y = 9.10X – 34.67」となるようですね。

matplotlibの簡単な利用

最後に、散布図と今回得られた予測の直線をmatplotlibで描いてみます。

fig = plt.figure(figsize = (6, 6))
ax = fig.add_subplot(111)

#散布図のプロット
ax.scatter(_df,target_df, c="green")
ax.set_title(panda_box.feature_names[select_x] + ' vs MEDV')
ax.set_xlabel(panda_box.feature_names[select_x], fontsize = 14)
ax.set_ylabel('MEDV', fontsize = 14)
ax.grid(True)

#直線の描画
w1 = np.linspace(X.min(), X.max(), 100)
z  = reg.coef_ * w1 + reg.intercept_
z = z.reshape(-1,1)
z = z.reshape(-1,1)
ax.plot(w1, z, c="orange")

今回、matplotlibで直線を描くことを学びました。

直線を描くためには、先ほど導いた式のXに値を入れていけば直線を描くことができます。まずは、等間隔のXの値を作成します。numpyのlinespaceという機能で連続的な値を作成することができます。

「X.min()」はXの最小値、「X.max()」はXの最大値を表していて、100が、分割数です。そのため、ここではXの最小値からXの最大値までを100等分した数値を得られます。

※本当は、直線なので、２個のXの値（最小値と最大値）だけで直線をひくことは出来ます。

このXの等間隔の値をw1に配列として入れます。

この配列を「z = reg.coef_ * w1 + reg.intercept_」と、式に入れることで、予測値zの配列が得られます。

このw1に対するzを図にplotすることで直線を描くことができます。

次は、最小二乗法について詳細に勉強したいと思います。