多項式回帰、もう少し色々とやってみました。
前回はテストデータへの精度も出していなかったね。
前回、多項式回帰について勉強して、グラフにするところまではやっていましたが、肝心のテストデータへの精度を求めることはしていませんでした。今回は、2次元以上の多項式回帰を行ったり、テストデータへの精度がどのように変化しているのかなどをプログラムして確かめました。
前回の多項式回帰についての記事はこちらをご参考ください。

こんな人の役に立つかも
・機械学習プログラミングの勉強をしている人
・多項式回帰について勉強している人
・scikit-leranで多項式回帰を実装しようとしている人
データのべき乗化をする関数の作成
何回もデータをべき乗化する必要が出てきましたので、PolynomialFeaturesのデータ変換の部分を関数としてまとめました。
まずはimport〜ボストンデータ読み込みまでを行います。
from sklearn.datasets import load_boston
from sklearn import linear_model
from sklearn.preprocessing import PolynomialFeatures
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
panda_box = load_boston()
X = panda_box.data
y = panda_box.target
#0:CRIM 1:ZN 2:INDUS 3:CHAS 4:NOX 5:RM 6:AGE 7:DIS 8:RAD 9:TAX 10:PTRATIO 11:B 12:LSTAT
X = X[:,[5]]
#訓練データとテストデータに分割(テストデータ25%)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state=0)べき乗化のプログラム
このような入力と出力としました。
入力:
deg:何乗までかを指定
data:変換するデータをここに入れます。
出力:
変換されたデータの二次元配列
from sklearn.preprocessing import PolynomialFeatures
def Poly(deg, data):
PF = PolynomialFeatures(degree = deg, include_bias=False)
PF.fit(data)
trans_data = PF.transform(data)
return trans_dataこれで気軽にべき乗できるね。
線形回帰はどうだったか?
変換していないデータ、「X_train」で訓練した線形回帰です。
これは、単純な単回帰です。単回帰についてはこちらの記事もご参考ください。

#通常の線形回帰
linear = linear_model.Ridge(alpha=0).fit(X_train,y_train)
print("訓練データへの決定係数 :{:.3f}" .format(linear.score(X_train, y_train)))
print("テストデータへの決定係数:{:.3f}" .format(linear.score(X_test, y_test)))訓練データへの決定係数 :0.488
テストデータへの決定係数:0.468未知データへの精度は46%くらいですね。
2次元以上の時は?
前回は、グラフを描いて回帰線がどのようになっているかをみましたが、今回は精度を出したいので、次のように訓練をしてscoreで結果を出すのみです。
#訓練データとテストデータを2次元の特徴量に
X_train_2deg = Poly(2, X_train)
X_test_2deg = Poly(2, X_test)
#線形回帰を訓練
reg = linear_model.Ridge(alpha=0).fit(X_train_2deg,y_train)
#精度を表示
print("訓練データへの決定係数 :{:.3f}" .format(reg.score(X_train_2deg, y_train)))
print("テストデータへの決定係数:{:.3f}" .format(reg.score(X_test_2deg, y_test)))訓練データへの決定係数 :0.548
テストデータへの決定係数:0.547一気に54%まで上昇したね。いい感じ。
二次関数で近似するだけで結構未知データへの精度が上昇しました。
調子に乗って3次以上もやってみようと思います。
#訓練データとテストデータを2次元の特徴量に
X_train_3deg = Poly(3, X_train)
X_test_3deg = Poly(3, X_test)
#線形回帰を訓練
reg2 = linear_model.Ridge(alpha=0).fit(X_train_3deg,y_train)
#精度を表示
print("訓練データへの決定係数 :{:.3f}" .format(reg2.score(X_train_3deg, y_train)))
print("テストデータへの決定係数:{:.3f}" .format(reg2.score(X_test_3deg, y_test)))訓練データへの決定係数 :0.565
テストデータへの決定係数:0.546あれ、訓練データへの精度は上がってるのに、未知のテストデータへの精度は二次の時より低くなってる。
次に、4次の時です。
#訓練データとテストデータを2次元の特徴量に
X_train_4deg = Poly(4, X_train)
X_test_4deg = Poly(4, X_test)
#線形回帰を訓練
reg3 = linear_model.Ridge(alpha=0).fit(X_train_4deg,y_train)
#精度を表示
print("訓練データへの決定係数 :{:.3f}" .format(reg3.score(X_train_4deg, y_train)))
print("テストデータへの決定係数:{:.3f}" .format(reg3.score(X_test_4deg, y_test)))訓練データへの決定係数 :0.585
テストデータへの決定係数:0.525四次元の方がさらに訓練データへの精度は高いのに、テストデータへの精度は低くなってるね。
まとめ:多ければいいものでもない
4次までやると、徐々に訓練データへは精度が高くなりますが、テストデータへの精度が悪くなっています。
これは、典型的な「過学習」ということになります。過学習は、訓練データに合わせすぎて未知データの予測が正しくできない、という状態ですので、このままモデルを複雑にしても、精度の向上が望めないことがわかります。
10次元も試してみましたが、3次元の時よりは少し精度が向上しましたが、2次元の時の方が良い精度でした。
ちなみに、4次元の回帰線を表示してみるとこのようになりました。
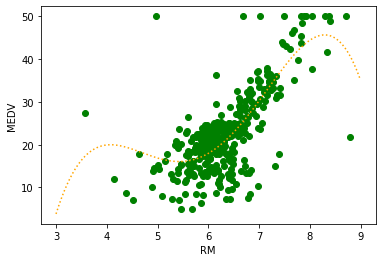
なんでも多ければいいってものでもないんだね。

