ビニングに続きて、特徴量を増やしてモデルを複雑にする、多項式回帰について学びました。
Xの二乗とかでも回帰できると便利だね。
今回は、ビニングに続いて、一つの特徴量でより複雑なモデルを構築するための手法の一つである、多項式回帰について学びました。以前、回帰の勉強をしようと色々検索していた時、回帰の基本は、線形モデルで、一つの特徴量に対してグラフ化するときは、回帰線は直線でしか表現できないはずなのに・・・非線形なことをしてる、と思われる事例がたくさん出てきて混乱してました。今回、多項式回帰を勉強して納得しました。
こんな人の役に立つかも
・機械学習プログラミングを勉強している人
・機械学習の多項式回帰を勉強している人
・scikit-learnで多項式回帰をしたい人
多項式回帰について
まず、単回帰はこんな形でした。
y=ax + b
傾き一つ、切片ひとつの形です。
これは、
y=w0 + w1x
のように書き直すことができます。この式(直線の式)をデータのばらつきに当てはめるのが単回帰の目的でした。そのために、最小二乗誤差を用いて、データのばらつきの中から最適な直線の傾き(w1)と切片(w0)を求めるというものでした。
単回帰は大丈夫。
次に、
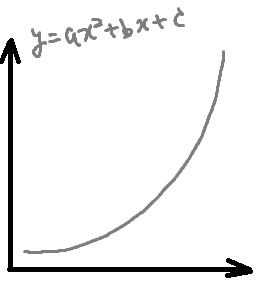
y=ax2 + bx + c
は二次関数になります。
もはや直線ではなくなってしまいます。xという説明変数についてxの二乗を追加しているので曲線で表現することができますが、これは線形ではなくなってしまいます。
ここで、この二次関数を
Y= a w1 + b w2 + w0
のように書き換えてみます。
重回帰の式に似ているね。
Xの二乗の部分を新しい特徴量とみなすと、重回帰と同じようにすることができます。
重回帰はこんな感じでした。
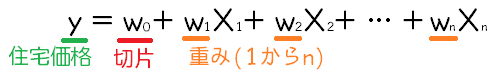
一つの特徴量で、冪乗を違う特徴量とみなして重回帰をする、イメージだね。
これで、一つの特徴量について、より複雑なモデルとすることができます。ボストンの住宅価格データのRMの多項式回帰を試してみたいと思います。
多項式回帰をプログラミング
プログラムに際して、ボストンの住宅価格データ、「RM」の特徴量を題材にします。
まずは、importからボストン住宅価格データ読み込みまでです。
特徴量(今回はRM)のべき乗の特徴量を作成するためには、scikit-learnの「PolynomialFeatures」という機能を利用します。ここでimportしておきます。
データ読み込みの時には、「X = X[:,[5]]」のように、部屋数データ「RM」のみのデータに変換しています。この点は、特徴量の選択についての記事でも書いていますので、ご参考ください。

from sklearn.datasets import load_boston
from sklearn import linear_model
#べき乗を作るためPolynomialFeaturesをimport
from sklearn.preprocessing import PolynomialFeatures
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
panda_box = load_boston()
X = panda_box.data
y = panda_box.target
#0:CRIM 1:ZN 2:INDUS 3:CHAS 4:NOX 5:RM 6:AGE 7:DIS 8:RAD 9:TAX 10:PTRATIO 11:B 12:LSTAT
X = X[:,[5]]
#訓練データとテストデータに分割(テストデータ25%)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state=0)次に、PolunomialFeaturesで「RM」を「RM、RMの二乗」と二つの特徴量に変換します。
PolynomialFeaturesでのデータ変換は、「作成」→「訓練(fit)」→「変換(transform)」の三段構成でできます。「degree=2」が二乗までのデータという意味です。
niji = PolynomialFeatures(degree = 2, include_bias=False)
niji.fit(X_train)
niji_fitted = niji.transform(X_train)PolynomialFeaturesで変換したデータを確認してみます。
print(niji_fitted.shape)
print(niji_fitted[:3])二乗したデータの列が増えていることが確認できます。
(379, 2)
[[ 5.605 31.416025]
[ 5.927 35.129329]
[ 7.267 52.809289]]最後に、リッジ回帰(alpha=0なので線形回帰)でデータに対してどのような回帰の線を引いているか確認します。
「line」は、X軸の左端から右端までを1000分割した配列になっていて、グラフを描く時に利用します。「line_niji」は、lineをpolunomialFeaturesで特徴量を変換したものです。この「line_niji」を線形モデルのpredictへ入れると、そのXの値の住宅価格予測を得ることができます。「line」をmatplotlib、plotのX軸とすることで今回の二次の曲線を描くことができます。
#Ridge回帰を作成して訓練させる
reg = linear_model.Ridge(alpha=0).fit(niji_fitted,y_train)
print("訓練データへの決定係数 :{:.3f}" .format(reg.score(niji_fitted, y_train)))
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(X_train, y_train, color="green")
#訓練した回帰線を描くための処理===
line = np.linspace(3,9,1000,endpoint=False).reshape(-1,1)
line_niji = niji.transform(line)
#===
ax.plot(line, reg.predict(line_niji), color='orange' , linestyle = "dotted")
ax.set_xlabel("RM")
ax.set_ylabel("MEDV")訓練データへの決定係数 :0.548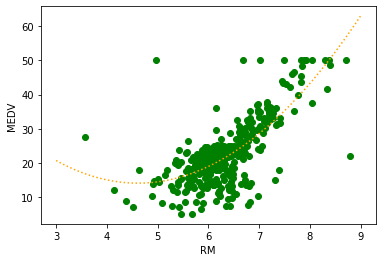
二次関数になってる。ちょっと感動しました。
次回は、多項式回帰した場合と、通常の単回帰でどのように精度が変わるのかまでみていきたいです。

