興味のままにPyTorchのチュートリアルをやってました。
いきなりGANとかやってたよね。
PyTorchのチュートリアルに興味を引くものがたくさんありまして、一番最初「A 60 Minute Blitz」をやったあと、色々手をつけてしましました。改めてチュートリアルを眺めてみると、「Learning PyTorch」という内容の項目がもういくつかあることに気がつきました。最初は、numpyのみでニューラルネットワークを構築と興味深いものとなっています。ということで、チュートリアル「LEARNING PYTORCH WITH EXAMPLES」をやっていきます。
numpyでウォームアップ
どうやら、tensorを利用する前に、numpyのみでネットワークを実装してみるらしいです。
ご存知の通り、numpyは、N次元の配列を提供してくれます。そして、これらの配列を操作するための便利な機能をたくさん提供してくれます。コンピュータサイエンスの分野ではもう一般的なフレームワークです。
numpyの操作を利用して、順伝播と逆伝播を手動で実装して2層のネットワークを作成してみます。
この2層(入力層、中間層、出力層)のネットワークは、yというランダムに生成された10個の出力へ近づけていく、というちょっと抽象的な内容になっています。
numpyの機能おさらい
今回利用されているnumpyのメソッドについてまずは復習です。
・「random.randn」メソッド
平均0、分散1の「標準正規分布」からランダムな値を作成する機能になります。
・「dot」メソッド
内積や行列の掛け算を行うことができます。
・「maximum」メソッド
maximum(比較する要素,比較する基準)という機能です。maximum(h,0)とすることで、0より大きいhは数値が返され、0以下のhは0が返されます。これは、「ReLU関数」と同じ動作になります。
・「square」メソッド
二乗の操作を行います。
・「T」メソッド
行列の転置の操作を行います。
実装
今回のニューラルネットワークは、入力1000次元、中間層100次元、出力10次元となるような構造です。
ネットワークの定義と初期化
# -*- coding: utf-8 -*-
import numpy as np
# N :バッチサイズ
# D_in :入力次元数
# H :隠れ層の次元数
# D_out:出力次元数
N, D_in, H, D_out = 64, 1000, 100, 10
# ランダムな入力データの作成
x = np.random.randn(N, D_in)
#ランダムに目標とする答えであるyを作成
y = np.random.randn(N, D_out)
print(x.shape)
print(y.shape)入力データとして、64個のデータ(特徴量1000次元)のデータを定義しました。入力データは、標準正規分布から選択されたランダムな数値の行列です。
また、目指すべき正解のデータとしても64個(10次元)のデータを定義しました。64個の答えデータは、標準正規分布から選択されたランダムな数値の行列です。
(64, 1000)
(64, 10)答えとか入力がランダムな値なのですごく抽象的感じがします。
入力データからネットワークが出力する数値を、ここで定義された64個のyのデータに向かって、重みを更新していくような処理になります。
# 重みをランダムに(標準正規分布の値から)初期化
w1 = np.random.randn(D_in, H)
w2 = np.random.randn(H, D_out)
print(w1.shape)
print(w2.shape)(1000, 100)
(100, 10)重みは次の図のように、ノードが次の層のノードへ全結合しているため、行列で表現できます。w1という重みテーブルには1000×100の重みが表現されることになります。
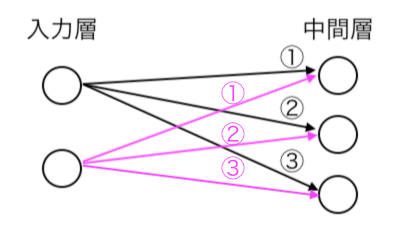
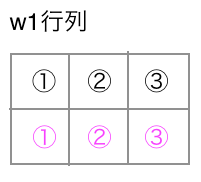
シンプルに上の図のように2入力ノードから3中間ノードへの重みは次のテーブルのような行列で表現できます。
損失の減少を視覚化するため、チュートリアルプログラムにリスト、「loss_list」を追加しています。二乗誤差の表示のところで、「loss」をapeendして、毎回の損失の数値をリストに蓄積していきます。
#損失記録用のリスト
loss_list = []
#学習率 0.000001
learning_rate = 1e-6
for t in range(500):
#①順伝播(yを予測するフェーズ)
#重みw1とxの掛け算(行列の掛け算)
h = x.dot(w1)
#活性化関数reluを適用
h_relu = np.maximum(h, 0)
#中間層の出力にw2の重みを掛け算して予測出力を得る
y_pred = h_relu.dot(w2)
#二乗誤差の計算と、誤差の表示
loss = np.square(y_pred - y).sum()
print(t, loss)
loss_list.append(loss)
#②逆伝播:w2とw1の勾配を計算する。
grad_y_pred = 2.0 * (y_pred - y)
grad_w2 = h_relu.T.dot(grad_y_pred)
grad_h_relu = grad_y_pred.dot(w2.T)
grad_h = grad_h_relu.copy()
grad_h[h < 0] = 0
grad_w1 = x.T.dot(grad_h)
#③重みの更新(勾配降下法)
w1 -= learning_rate * grad_w1
w2 -= learning_rate * grad_w2①は、順伝播です。とにかく入力してみて、今の重みでの答えを得るような処理になります。
そのあとの誤差を算出する部分では、二乗誤差を計算していますが、誤差関数というほどのものではなく、単純に今の予測値がどれほど正解のyと離れているかを計算して指標として表示している部分になります。
②では、逆伝播を行なっています。行列の計算で勾配を求めるような計算をしているようですね。w2の勾配、w1の勾配がここで算出されます。
勾配の計算のところは・・・行列の計算などでこのように求めることができるのですね 笑
勾配の計算を雰囲気でスルーしたね。
PyTorchの自動微分は素晴らしいということに気づきました。
③の重みの更新は、勾配降下法をそのまま計算して、重みを更新しています。
勾配降下法については、こちらで考察しましたので、ご参考ください。

このプログラムを実行することで500回の訓練が行われます。1回の訓練で64個全てのデータを利用しているので、バッチ学習ということができそうです。
==省略==
498 7.856321162650611e-15
499 7.544662867421618e-15損失の減少をmatplotlibでグラフ化しました。
import matplotlib.pyplot as plt
plt.xlabel("train num")
plt.ylabel("loss")
plt.plot(range(500),loss_list)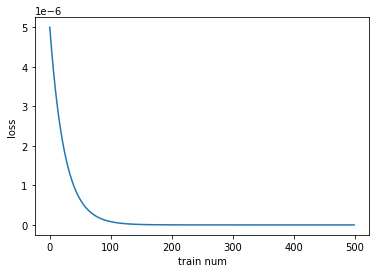
ニューラルネットワークの重みが最初に定義したランダムなyの出力へと近づいて行っている様子がみられます。
今回のプログラムはGitHubにて確認いただけますので、ご利用ください。
続きの記事はこちらです。



