勾配降下法の仕組みについて考察、誤差関数の定義や勾配の降下を確認

前回に引き続き、ニューラルネットワークの中の仕組みを理解しようと奮闘しています。今回は、勾配効果法について私なりの考察を行ってみました。

こんな人の役に立つかも

・機械学習プログラミングを勉強している人

・ニューラルネットワークの勉強をしている人

・勾配降下法の仕組みについて知りたい人

シンプルな例

w1 × x1 = target

という関係式において、次の２つのデータが存在するとします。

data1 : x1 = 2, target = 5

data2 : x1 = 1, target = 3

import matplotlib.pyplot as plt
import numpy as np

fig = plt.figure(figsize = (5, 5))
ax = fig.add_subplot(111)

plt.xlim(0,7)
plt.ylim(0,7)
plt.xlabel("x1")
plt.ylabel("target")
plt.grid(which='major',color='darkgray',linestyle='-')
plt.scatter(2,5)
plt.scatter(1,3)

data1をもとにw1を求めると、w1=2.5となり、

data2をもとにw1を求めると、w1=3となります。

fig = plt.figure(figsize = (5, 5))
ax = fig.add_subplot(111)

plt.xlim(0,7)
plt.ylim(0,7)
plt.xlabel("x1")
plt.ylabel("target")
plt.grid(which='major',color='darkgray',linestyle='-')
plt.scatter(2,5)
plt.scatter(1,3)
x_axis = np.linspace(0,7,7)
plt.plot(x_axis, 5/2*x_axis)
plt.plot(x_axis, 3/1*x_axis)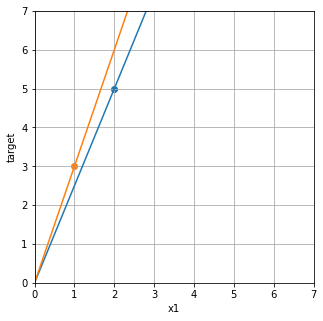

この２つのデータをに対してちょうどよい感じの関係式のw1はどうなるでしょうか？

下のグラフのような中間くらいの線が引きたくなりますね。これは私の感覚で設定したw1です。

fig = plt.figure(figsize = (5, 5))
ax = fig.add_subplot(111)

plt.xlim(0,7)
plt.ylim(0,7)
plt.xlabel("x1")
plt.ylabel("target")
plt.grid(which='major',color='darkgray',linestyle='-')
plt.scatter(2,5)
plt.scatter(1,3)
x_axis = np.linspace(0,7,7)
plt.plot(x_axis, 2.7*x_axis, color="green")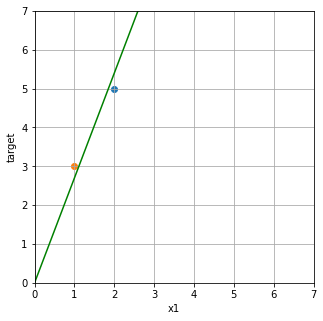

前回勉強した、二乗誤差を導入してこのちょうど良いw1を求めていきたいと思います。

今回は、data1とdata2が与えられていますので、それぞれの誤差の平均をとった「平均二乗誤差」という誤差を採用します。二乗誤差を平均することで、今ある現実データに対する平均的な誤差を最小にしていくというアプローチです。

まずは、平均二乗誤差が今回、どのような式になるかを見ていきます。

平均二乗誤差を定義しよう

誤差関数の定義

勾配と誤差についての知識は、前回の記事もご参考ください。

二乗誤差の定義を思い出す

二乗誤差(square_error)は次のようにしました。

square_error = (predict – target)^2

square_error = ((w1 * x1) – target)^2

data1とdata2に対する二乗誤差

今回のdata1[2,5]とdata2[1,3]の具体的な二乗誤差は次のように求められます。

・data1の二乗誤差 
(2w1 – 5)^2 = 4w1^2 – 20*w1 + 25 ・・・①

・data2の二乗誤差
(1*w1 – 3)^2 = w1^2 -6w1 + 9 ・・・②

data1とdata2を平均した平均二乗誤差

今回は、二つのデータがあるので、二乗誤差を平均二乗誤差というものにします。平均二乗誤差は、「MeanSquareError(MSE)」とよばれたりします。

平均二乗誤差(MSE) = ① + ② / 2

実際に、代入して計算すると次の二次関数になります。

mean_square_error = (5w1^2 – 26w1 + 34) / 2 = 2.5*w1^2 – 13w1 + 17

これをグラフにしてみましょう。

fig = plt.figure(figsize = (5, 5))
ax = fig.add_subplot(111)

plt.xlim(-5,10)
plt.ylim(-5,100)
plt.xlabel("w1")
plt.ylabel("mean_square_error")
plt.grid(which='major',color='darkgray',linestyle='-')
x_axis = np.linspace(-5,10,25)
plt.plot(x_axis, 2.5*x_axis*x_axis - 13*x_axis + 17, color="green")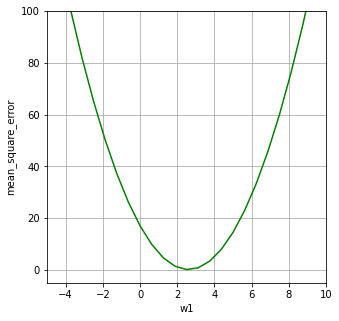

data1とdata2に対する平均誤差に完全にw１を最適化させると、平均二乗誤差w1が0のところで一番良いw1となります。

ということは、「接線の傾き」=「平均二乗誤差の微分値」=「勾配」を0にすれば良いことになります。

5*w1 – 13 = 0

をとけば良いことになります。

w1 = 13/5
print(w1)

2.6

ということで、data1とdata2に対してw1*x1でちょうど良い予測線を引こうとすると、w1が2.6であることがわかります。

でも、少し考えてみると、data1とdata2以外にdata3とdata4が新たに判明しました。となった時に、ここで求めたw1=2.6は最適な値でしょうか？？

w1=2.6という値は、data1とdata2しかない時のみの最適なw1であって、data3やdata4に対しても同じように最適なw1となっているとは限りません。

そのため、data1とdata2の誤差に対して、勾配が0になる点に合わせてしまうということはデータに対してフィットしすぎてしまう「過学習」の状態であると考えることができます。

そこで、勾配降下法という方法で、少しづつw1を動かして、過学習しない程度にw1を動かしたいというイメージになります。

勾配降下法を使ってみる

ここからは、勾配降下法で誤差を最小にしていきます。

勾配降下法は、今の重みw1を勾配に学習率をかけたもので更新するという仕組みになっています。次のような式で表現するのですが、とてもシンプルです。

出てくる値は、

①現在の重みw1

②学習率μ

③勾配：上の図の赤枠です。

③∂L / ∂w1 が平均二乗誤差である「L」を重み「w1」で微分する、という意味なので、先に出てきた平均二乗誤差の微分値「5*w1 – 13」に相当します。

まずはw1=1からスタートしてみます。(適当に1としました。)

5*w1 – 13 の w1 に 1 を代入すると、

#平均二乗誤差の微分した式=勾配
gradient1 = 5*1 - 13
print(gradient1)

-8

fig = plt.figure(figsize = (5, 5))
ax = fig.add_subplot(111)

plt.xlim(-5,10)
plt.ylim(-5,100)
plt.xlabel("w1")
plt.ylabel("mean_square_error")
plt.grid(which='major',color='darkgray',linestyle='-')
x_axis = np.linspace(-5,10,25)
plt.plot(x_axis, 2.5*x_axis*x_axis - 13*x_axis + 17, color="green")
plt.plot(x_axis, -8*x_axis+14.5)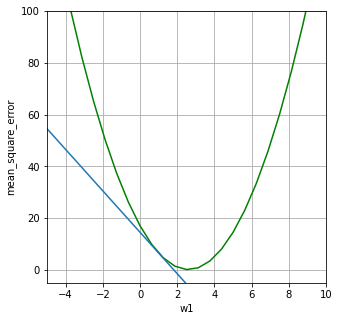

せっかくなので、接線もグラフ化してみました。

接線にする必要はないのですが、この傾きがマイナスというイメージがわかりやすそうなので接線を描いてみました。

先ほどの「重み更新の式」に当てはめると、

w1 – μ * (-8)

ということになります。

さらに具体的には、今w1が1なので、

1 – μ * (-8)

学習率μは手動で決める必要がある係数になります。式をみるとわかると思うのですが、この係数は一般的に0.001〜0.1などの数値を入れていき、今の勾配でどれくらい重みを更新していくかを設定することができます。

このμはニューラルネットワークでいう「learning_rate」というハイパーパラメータとなっています。

今回、μ=0.1としてみます。

w1 := 1 – 0.1 * (-8)

#重みの更新
w1 = 1 - 0.1 * -8
print(w1)

1.8

w1は1.8に更新されました。

もう一度、更新された重みから、同じ手順で重みの更新を行ってみましょう。

#勾配の算出
gradient2 = 5*1.8 - 13
print(gradient2)

-4.0

次は勾配が-4となりました。先ほどと同じように、重みを更新してみます。

w1 := 1.8 – 0.1 * (-4)

(参考 w1 – μ * 勾配)

#重みの更新
w1 = 1.8 - 0.1 * (-4)
print(w1)

2.2

w１が2.2になりました。同じように３回目の更新も行ってみましょう。

#勾配の算出
gradient3 = 5*2.2 - 13
print(gradient3)

-2.0

#重みの更新
w1 = 2.2 - 0.1 * (-2)
print(w1)

2.4000000000000004

何回か繰り返してみます。

#勾配の算出
gradient4 = 5*2.2 - 13
print(gradient4)
#重み
w1 = 2.4 - 0.1 * (gradient4)
print(w1)

-2.0
2.6

#勾配の算出
gradient5 = 5*2.6 - 13
print(gradient5)
#重み
w1 = 2.6 - 0.1 * (gradient5)
print(w1)

0.0
2.6

5回の繰り返しで2.6という重みに落ち着きました。本当はここまでやってしまうと完全にdata1とdata2の誤差に対する重みとなってしまうので、過学習です。そのため、実際には、訓練の回数を調整したりします。

勾配降下方では、このように、勾配を利用して重みを最適な方向へ移動させていくことができます。

現実的に利用するニューラルネットワークでは、何万というデータに対して重みを更新、また、今回は重みが１つだけなので、0を通る直線以外は表現できませんでしたが、もっと多くのパラメータを同様に調整することでより複雑なモデルを実現しています。

エポックとバッチ学習、オンライン学習

データの使い方として、data1のみで勾配を求めて、重みを算出、次にdata2を利用して勾配を算出、重みの更新、と一つづつ利用して重みを更新することもできます。このように一つづつデータを利用して重みを更新する方法が

「オンライン学習」

と呼ばれます。新たに入手したデータを追加して重みに反映させるようなやり方です。

それに対して、今回data1とdata2を全て利用して１回の重み更新を行う方法は

「バッチ学習」

と呼ばれています。

いづれにしても、「全ての訓練データを使い切る＝１エポック」ということになります。今回の例では、data1とdata2の両方を利用して重みを更新し終わった時点で1エポックと呼ぶことになります。