窓関数というものが出てきました。難しいことはよくわかりません・・・
大体の概要をつかむ程度でいいんじゃないかな~
JUCEチュートリアルの「DSP」の項目、「Visualise the frequencies of a signal in real time」を進めていきます。周波数の可視化ということで、よくDAWのEQとかに表示されるようなリアルタイムでの周波数表示ができるような機能を、アプリを実装して学んでいきます。今回は、まずはFFTでの窓関数が何か調査を行いましたので、リンクや現状の理解を図で表現したりしてみました。
このチュートリアルは、「The fast Fourier transform」の内容を前提としている部分があります。本ブログでもチュートリアルを進めていますので、以下の記事もご参考ください。
進めている公式のチュートリアルのページはこちらです。
https://docs.juce.com/master/tutorial_spectrum_analyser.html
こんな人の役に立つかも
・JUCEチュートリアル「Visualise the frequencies of a signal in real time」をやっている人
・FFTの窓関数について調べている人
チュートリアルで作成するアプリ
スクリーンショットのように、DTMをやる人にはなじみのある周波数の表示ができます。縦軸が振幅、横軸が周波数となります。また、このアプリは、1秒間に30回の画面更新を行います。
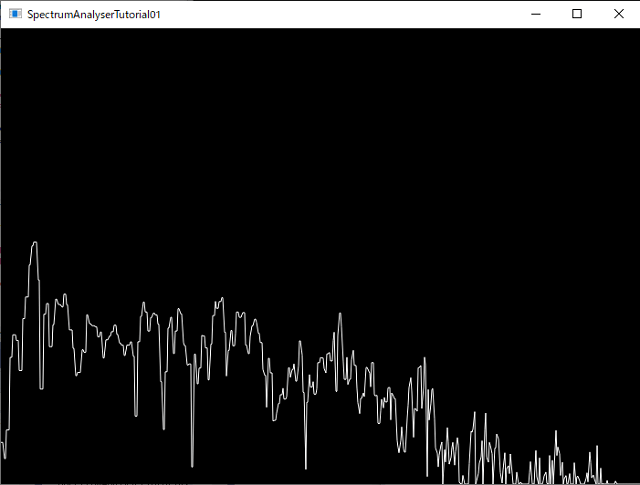
何となく雰囲気出てきましたね
FFTの窓関数について調査
前回のチュートリアルでは、窓関数を適用していませんでした。窓関数が何かを調査しました。
以下のサイトにお世話になりました。
https://www.logical-arts.jp/archives/124
前回のチュートリアルの実装例でみると、サンプリングレート44100Hz(1秒間に44100回のサンプリング)で1024サンプル周期のFFTだと、44100÷1024≒43.06となり、「43.06…Hz、86.12…Hz、…」と、43.06Hzの整数倍の周波数のサイン波やコサイン波で構成された周期波形でないと正確な周波数の振幅を取得できていないということになります。(フーリエ変換は、周期的な関数(音波など)を前提としているので)
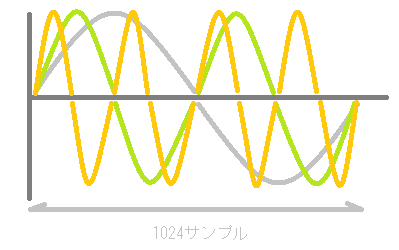
先に挙げた43.06…Hzとその整数倍の周波数以外の周波数をもつサイン波やコサイン波の場合、FFTは周期性がある波形として処理するので、波形に不連続性が生じてしまいます。
1024サンプルより大きい周期の場合と小さい場合を図にしてみました。

1024サンプルのところで波形の最初になるという前提でFFTは動作するので、周波数がずれると、このようないびつな形の波形が周期的に繰り返されているという前提で分析が行われます。このいびつな波形を周期的なサイン波やコサイン波へと分解するので、本来ないはずの周波数などが出現してきます。
窓関数は、このような周期的でない波形に掛け合わせることで、本来ないはずの周波数が出て来たりする点を改善しようというものです。
https://ja.wikipedia.org/wiki/%E7%AA%93%E9%96%A2%E6%95%B0
本格的には、周波数分解能とダイナミックレンジのバランスを調整する、みたいな難しい用語で表現されています。
窓関数を掛け合わせることで音の波形が変化する様子は次のサイトがわかりやすかったです。
https://www.fbs.osaka-u.ac.jp/labs/ishijima/FFT-06.html
窓関数にはいくつかの種類があり、「ハン窓」と「ハミング窓」がよく使われるようです。
プロジェクトの作成
デモアプリ実装のためのプロジェクトをProjucerで作成します。
Projucerの「Audio」のテンプレートを利用してプロジェクトを作成しました。※プロジェクト名は任意の名称にしておきます。
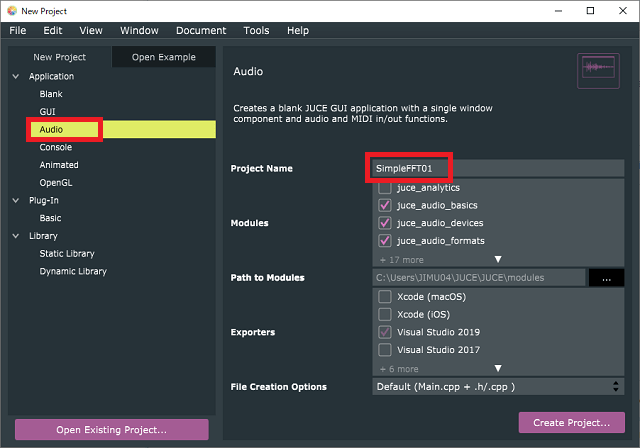
FFTを利用するので、DSPモジュールをプロジェクトに追加しておきます。
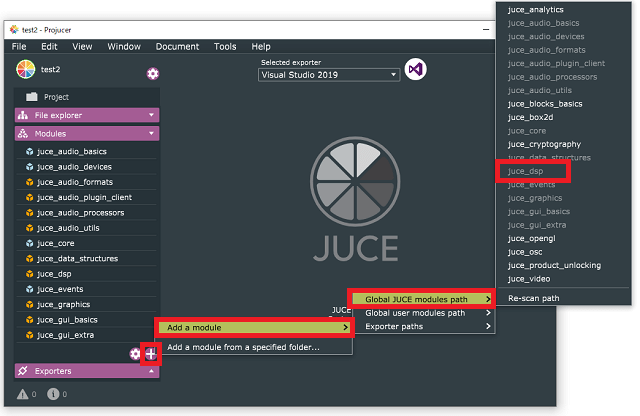
次回の記事で、実装についてまとめたいと思います。このプロジェクトを利用して周波数表示のアプリを実装していきたいと思います。

