JUCEプログラミング、The fast Fourier transform3、スペクトログラム描画処理の詳細

前回実装したスペクトログラムの表示アプリですが、フーリエ変換の結果をスペクトログラムとして表示する部分が結構複雑に感じましたので、その部分をより詳細に見ていきたいと思います。

前回の記事はこちらです。

公式のチュートリアルはこちらです。

https://docs.juce.com/master/tutorial_simple_fft.html

こんな人の役に立つかも

・JUCEチュートリアル「The fast Fourier transform」をやっている人

・スペクトログラムのアプリをJUCEで実装したい人

drawNextLineOfSpectrogram関数

このアプリの描画は、timerCallbackで以下のdrawNextLineOfSpectgram関数が呼び出され、GUIに表示するためのスペクトログラム画像を作成、その後、repaintによってpaint関数で画像がGUIに描画されるという処理が１秒間に６０回実行されます。

今回は、スペクトログラムの画像がどのように作成されるかを詳細に追います。

void MainComponent::drawNextLineOfSpectrogram()
{
    //[1]画像を左へずらす処理です。
    auto rightHandEdge = spectrogramImage.getWidth() - 1;
    auto imageHeight = spectrogramImage.getHeight();

    spectrogramImage.moveImageSection(0, 0, 1, 0, rightHandEdge, imageHeight);

    //[2]フーリエ変換で周波数の情報を得ます。
    forwardFFT.performFrequencyOnlyForwardTransform(fftData.data());

    //[3]現在時間のスペクトログラムを作成します。
    auto maxLevel = juce::FloatVectorOperations::findMinAndMax(fftData.data(), fftSize / 2);

    for (auto y = 1; y < imageHeight; ++y)
    {
        auto skewedProportionY = 1.0f - std::exp(std::log((float)y / (float)imageHeight) * 0.2f);
        auto fftDataIndex = (size_t)juce::jlimit(0, fftSize / 2, (int)(skewedProportionY * fftSize / 2));
        auto level = juce::jmap(fftData[fftDataIndex], 0.0f, juce::jmax(maxLevel.getEnd(), 1e-5f), 0.0f, 1.0f);

        spectrogramImage.setPixelAt(rightHandEdge, y, juce::Colour::fromHSV(level, 1.0f, level, 1.0f));
    }
}

このプログラムは大まかに[1]で画像を左へ1ピクセルずらします。[2]で、フーリエ変換をして現在サンプル(1024個分の時間間隔）の周波数情報を取得します。[3]で取得した周波数情報を幅1ピクセルの画像一番右の縦の線として描画します。

[1]と[2]は理解できるとして、[3]の計算部分では、周波数情報をスケーリングしていて、ぱっと見理解しづらかったので、計算を確認しながら見ていきます。

1.画像を左へずらす処理

RightHandEdge変数には、画像幅から1ピクセル引いた値を格納しておきます。

imageHeight変数は画像高さそのままの値を格納します。

これらの値を使い、moveImageSection関数で画像を1ピクセルずらします。

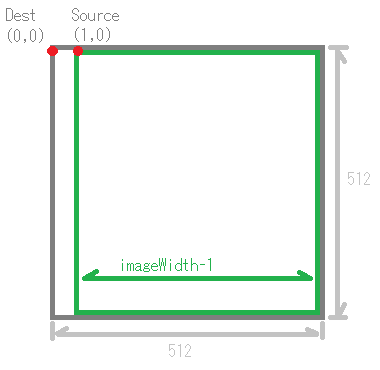
第一、第二引数の(0,0)が移動先原点、第三引数、第四引数が移動元の原点で、第五引数、第六引数に移動する画像の幅、高さを指定します。動作としては、1ピクセル小さい幅の画像を左に移動しています。

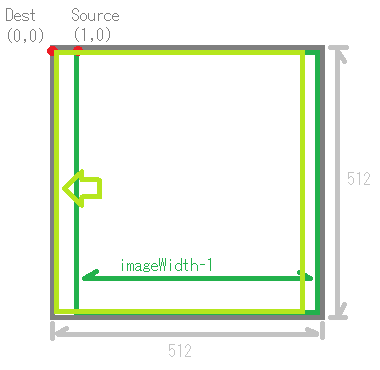
2.FFTを実行

以下のプログラムの部分になります。

//[2]フーリエ変換で周波数の情報を得ます。
    forwardFFT.performFrequencyOnlyForwardTransform(fftData.data());

performFrequencyOnlyForwardTransform関数で、512個の周波数領域のデータが得られます。

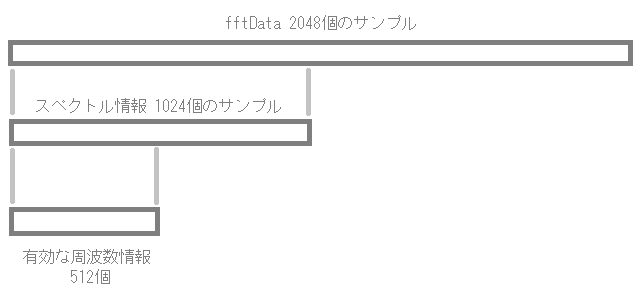
performFrequencyOnlyForwardTransform関数の挙動については、以前の記事に詳細に書きましたので、ご参考ください。

ここでは、雑に、以前の記事で作成した画像をはりつけて、出力の内容の確認とします。

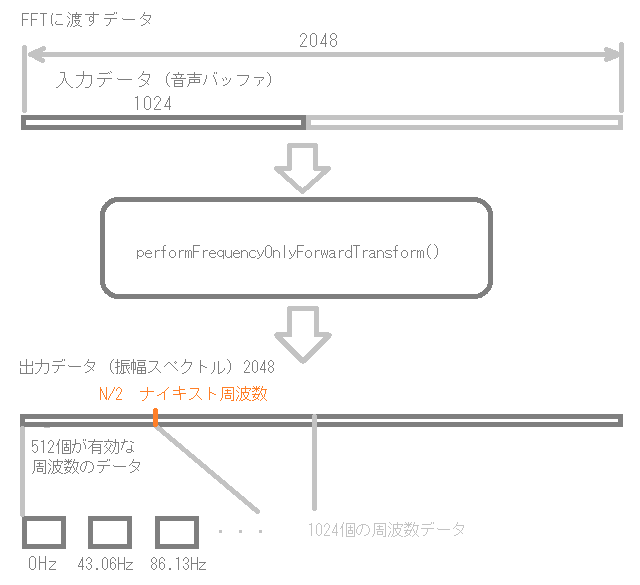
このように、43.06…Hz刻みの周波数のデータへと変換されます。

現在時間のスペクトログラムを作成

次のプログラムの部分となります。この処理で、先ほどずらした一番右の現在時間のスペクトル画像（幅1ピクセル、高さ512ピクセルの画像）を作成していきます。

    //[3]現在時間のスペクトログラムを作成します。
    //[3-1]周波数のデータから、最小値と最大値を取得します。
    auto maxLevel = juce::FloatVectorOperations::findMinAndMax(fftData.data(), fftSize / 2);

    //[3-2]幅1ピクセルの画像を作成します。
    for (auto y = 1; y < imageHeight; ++y)
    {
        auto skewedProportionY = 1.0f - std::exp(std::log((float)y / (float)imageHeight) * 0.2f);
        auto fftDataIndex = (size_t)juce::jlimit(0, fftSize / 2, (int)(skewedProportionY * fftSize / 2));
        auto level = juce::jmap(fftData[fftDataIndex], 0.0f, juce::jmax(maxLevel.getEnd(), 1e-5f), 0.0f, 1.0f);

        spectrogramImage.setPixelAt(rightHandEdge, y, juce::Colour::fromHSV(level, 1.0f, level, 1.0f));
    }

[3-1]では、まず、得られたデータの最も大きい数字と最も小さな数字を取得します。findMinAndMax関数は、JUCE::FloatVectorOperationsクラスのstaticな関数です。返り値は、juce::Rangeのオブジェクトとして得られます。今回は、512個(fftData/2個)のfloat配列から周波数の振幅スペクトルデータの最大と最小を取得してきます。

[3-2]では、画像の高さ回数繰り返して、1ピクセルずつ、振幅スペクトルの数値を色に変換して書き込んでいきます。FFTの結果は、512個の配列に43.06…Hzの間隔で比例的に並んでいるだけです。実際の表示は、対数スケールのように、高い周波数は表示周波数の刻みを細かく、低い周波数は表示間隔を広くするような表示がより人の間隔に近く、自然になります。

このスケーリングを行うために、skewedProportionY、fftDataIndex、levelという変数を計算しています。

まず、skewedProportionYがどのような値になるかを確認していみます。

auto skewedProportionY = 1.0f - std::exp(std::log((float)y / (float)imageHeight) * 0.2f);

ここからは、google colaboratoryで、Pythonで計算しています。↑の式の「y/512」は、yが512に近づくほど、式の答えが1に近くなります。これは、繰り返しが進んで、画像の下のピクセルになるほど、この式の値は1に近くなる性質があります。

ここからは実際にgoogle colaboなどで計算するとわかりやすいかもしれません。以下、はPythonでのプログラムになります。

import matplotlib.pyplot as plt
import math

#「y / 512」の配列を作成
list = []

for num in range(1,512):
  list.append(num/512)

print(list)
plt.plot(list)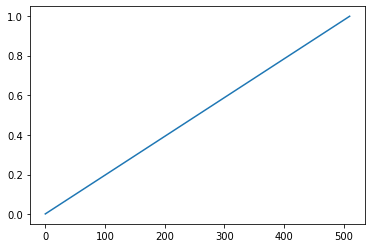

512回繰り返すほど1に近づいていくグラフです。

次に、この値を引数にして、std::logにて対数をとります。

「std::log((float)y / (float)imageHeight)」の部分です。

#LOG(y/512)の計算
list2 = []

for x in list:
    list2.append(math.log(x))

print(list2)

plt.plot(list2)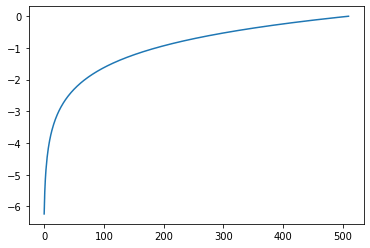

このlog関数で、yが増えるほど値の増加量が少なくなっていくグラフのような結果が得られます。

次に、「std::exp(先の結果) * 0.2f)」の部分です。

#EXP(LOG * 0.2)の計算
list3 = []
for x in list2:
  list3.append(math.exp(x * 0.2))

print(list3)

plt.plot(list3)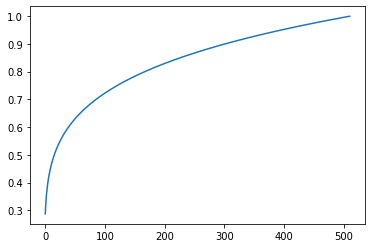

少しだけなだらかになりました。

そして、「1-(先の結果)」とすることで、skewedProportionYの値となります。

# 1 - EXP　の計算(skewedProportionY)
list4 = []
for x in list3:
  list4.append(1 - x)

print(list4)

plt.plot(list4)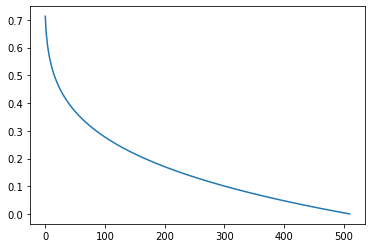

1から引くことで、グラフがX軸方向に反転しました。Y軸の値が0~1の間の数値となっているので、これを0～512の整数に変換することで、fftDataIndexの値となります。jlimit関数で0～512の値の中の数字という制限は設けているものの、計算としては、512をかけているだけです。

#skewedProportionY * 512
list5 = []
for x in list4:
  list5.append((int)(x * 512))

print(list5)

[364, 343, 328, 317, 309, …..,2, 2, 2, 2, 2, 1, 1, 1, 1, 1, 0, 0, 0, 0]

fftDataIndexの値は、FFTの結果の512個あるデータの何番目のデータを見るのか、というFFTデータ配列のインデックスが得られます。このインデックスからFFTの結果の配列を見ることで、参照する周波数のスケーリングを今回のグラフのように参照することができるようになります。

例えば、y=1のときは、fftDataIndexは364になるので、364番目のFFTのデータ、これは43.06Hz×364≒15673.84Hzのデータを参照することになります。画像の一番上のピクセル、y=1のときは15673Hzのデータを表示することになります。次にy=2のとき、画像の上から２番目のピクセルでは、43.06Hz×343≒14769Hzのデータを表示することになります。これを続けて、画像のピクセルが下に進むほど、インデックス番号が連続して登場するようになります。たとえば、「2」と「１」は5回づつ繰り返されています。これは、下の方のピクセルは何個かにわたって同じ周波数を表示していることになります。

スケーリングして取得するFFTデータの配列の番号がわかったら、データを取得して、level変数の計算に利用します。ここで得られるデータは各周波数の振幅のはずなので、振幅の大きさとして0～1にスケーリングします。

auto level = juce::jmap(fftData[fftDataIndex], 0.0f, juce::jmax(maxLevel.getEnd(), 1e-5f), 0.0f, 1.0f);

jmap関数は、「第二引数～第三引数の範囲」の第一引数の値を「第四引数～第五引数」にスケーリングしたときの値に変換する関数です。今回は、０～最初に取得したFFTデータの一番大きな値までの値と0~1を対応付けます。

最後に、ピクセルとして画像に書き込みます。

spectrogramImage.setPixelAt(rightHandEdge, y, juce::Colour::fromHSV(level, 1.0f, level, 1.0f));

setPixelAt関数は、第一引数と第二引数の座標に第三引数の色のピクセルをセットする関数です。

rightHandEdgeは511なので、X方向で画像の一番右を示しています。ループでyの値が増えると下方向に座標が移動します。

ピクセルの色はfromHSV関数の第一引数と第三引数にlevel変数を入れることで決定します。hueとbrightnessを変化させることで色を表現しています。