DSPと言えば、フーリエ変換ですよね、使ってみたいです。
知識がないと結構厳しいよ~
JUCEプログラミングチュートリアル、「The fast Fourier transform」を始めました。FFTをDSPモジュールから利用するというチュートリアルです。DSPといえば、フーリエ変換でしょ、という軽いノリでチュートリアルを始めましたが、いろいろと何もわかっていなかった感が否めませんので、基本的な部分を調べたりするところから入っております^^;
公式のチュートリアルはこちらになります。
https://docs.juce.com/master/tutorial_simple_fft.html
※今回の記事は、個人的な考察も含むので、より厳密には間違っている点があるかもしれないことをご了承ください。
こんな人の役に立つかも
・JUCEチュートリアル「The fast Fourier transform」をやっている人
・モジュールとしてのフーリエ変換の知識が欲しい人
・JUCEのperformFrequencyOnlyFowardTransform関数について勉強している人
完成するデモアプリ
このチュートリアルを行うことで、最終的に次のようなデモアプリが完成します。
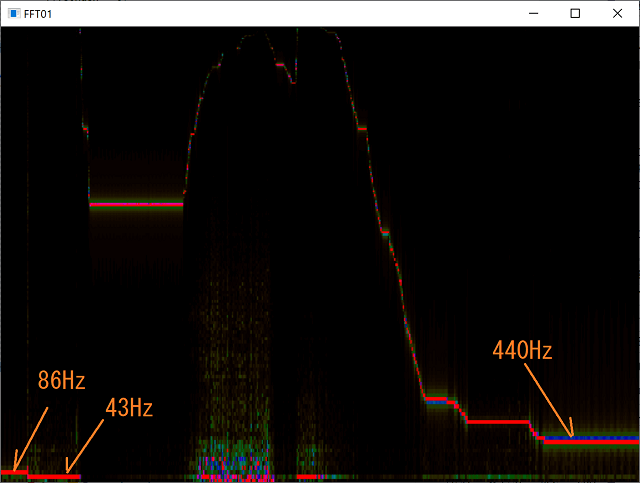
縦軸に周波数、横軸が時間、そして、色が音量を表現しています。オレンジの矢印の周波数は、パソコンのマイクに大きい音量でオシレータの発音している音を入れたときの表示です。
このアプリを紐解くことで、周波数を可視化できそうな予感がします。
FFTについて知る
FFTを使う上で、どのようなものかをすごく浅くおさらいしたいと思います。正直、まずはFFTがモジュールとして使えるので、入力がどのようなもので、出力がどうなるのか、がわかればまずはOKというような観点で進めていきたいと思います。崇高な数学的な事柄に関しては、今は触れずに、実装の理解をするという点を重視して行きたいと思います。
フーリエ変換について
フーリエ変換というもので、普段DAWなどで見ている波形を周波数領域へ変換する、というような、すごくざっくりとしたことは知っていたのですが、その仕組みまではよくわかりませんでした。
フーリエ変換(フーリエ級数展開)の基礎的な部分は、「複雑に見える波形はシンプルなサイン波(コサイン波)の組み合わせで似せることができる」ということのようです。次のサイトがとても分かりやすかったです。
https://kenyu-life.com/2019/06/03/fourierseries/
いくらか調べると、フーリエ変換といっても、数学的に文脈があるようで、すごくざっくりとした言葉のような気がしてきました。
私が普段思い描いていたDAWなどに表示されるような周波数の表示は実際のところ、離散フーリエ変換(DFT)というものの働きのようです。そしてこのDFTの理論の上にFFTがありました。
また、これらのフーリエ変換(というとおそらくDFTやFFTのことを言うのかな、と、この段階で感じ始めました。)にはfowardとinvertがあり、「foward」が順方向、という意味で、時間領域の音声データを周波数領域に変換するという動作で、「invert」が逆方向という意味で先ほどの逆の変換を行うようです。JUCEのFFTクラスの関数にはそれぞれ方向を指定するパラメータがあったり、Fowardを行う関数には、関数名にFowardが含まれていたりします。
FFT
FFT(高速フーリエ変換)は、計算方法をなんやかんや工夫して、計算速度早くした離散フーリエ変換(DFT)です。どちらにしろ、フーリエ変換と呼ばれる処理を実行するもので、プログラムに落とし込んでより実用的にしたのがFFTというような認識でしょうか。
今回のチュートリアルでは、JUCEのDSPモジュールに実装されているFFTというクラスを利用することで、FFTを手軽に使うことができそうです。(というものの、チュートリアルには、まだ最適化されていないけれど、将来的にはやるかも、というような表記も見られます^^;)
https://docs.juce.com/master/classdsp_1_1FFT.html#details
FFTの入力と出力
以下のサイトがとても的を射た内容で、アプリケーションを実装するうえで、FFTの入力と出力が分かればよい、というような観点からFFTについて解説をしてくれていました。非常に助かります。
https://www.logical-arts.jp/archives/112
ということで、入力には一般的に、2の累乗である1024個または2048個や4096個というサンプル数の音声データを与えるようです。これは、JUCEのチュートリアルでみるFFTの使い方も同じようです。
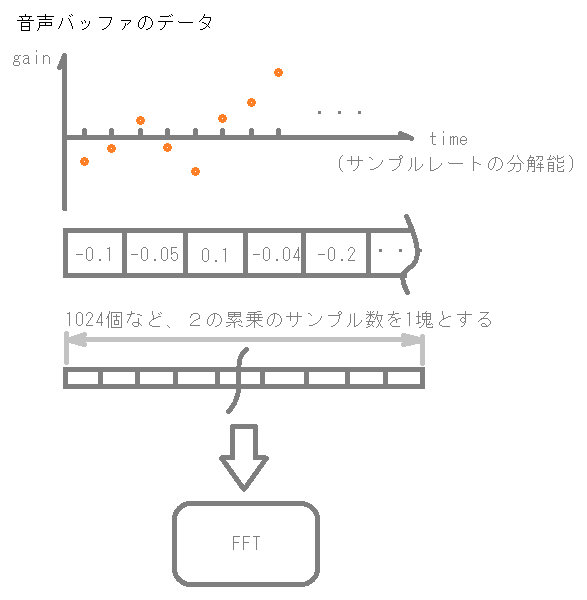
出力としては、一般的に実数と虚数がそれぞれ得られるようで、これらの値から、「振幅スペクトル」と「位相スペクトル」を計算するようです。実際、DAWとかでよく見る周波数の表示は、「振幅スペクトル」を表示しているということです。出力は、ライブラリによって形式が違ったりするらしいので、今回はJUCEのFFTクラスがどのような出力をするのか、確認する必要がありそうです。
JUCEのperformFrequencyOnlyFowardTransformの入出力
今回のチュートリアルでは、「performFrequencyOnlyForwardTransform()」という関数を利用することで、簡単に音声バッファを振幅スペクトルに変換した結果が得られるようです。この関数は、周波数を表示させたいときに気軽に周波数に変換できるように作られたようです。
この関数の入力は2の累乗個の音声サンプルデータを与えます。チュートリアルプログラムでは、1024個のサンプルデータを取得してFFTに与えますが、実際には、2048個の最初の1024個を埋めて渡しています。
そして、渡した配列データ自体を周波数領域のデータに変換してくれます。本当は、実数と虚数の二乗の和の平方根で振幅を求めるのですが、そこはもうできているみたいな雰囲気です。
現状の理解のイメージでは次のようになりました。
入力は、次のように最初の半分にフーリエ変換したい音声データを格納しておきます。
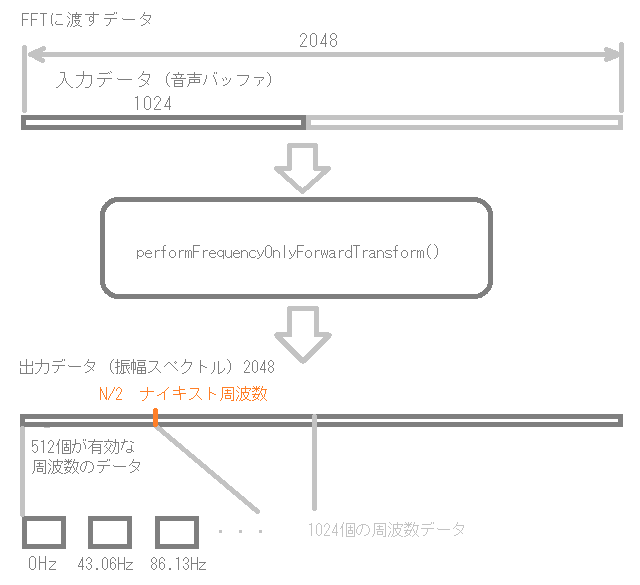
出力は、例えば、今回は、サンプリングレート44100で、サンプル数Nを1024個としたので、最終的に512個が有効な振幅スペクトルのデータとなるようです。
1秒間に44100サンプル数あるので、その1024個は「44100÷1024≒43.06Hz」です。そのため、今回のフーリエ変換では、約43.06Hzの整数倍の周波数の成分量が含まれているみたいなイメージだと考えています。

43と86のように、約43の倍数が今回の周波数の分解能だと思われます。(実際には縦軸が周波数の対数スケーリングをしてあるので、その影響の少なそうな43と86を見てみました。)
たぶん、こういうことだと思います・・・
離散フーリエ変換は、基本的にある決まった時間の範囲を基準として、その整数倍の周波数で構成されているという前提があるので、今回の場合は例えば10Hzという周波数は基本的に見ることができません。もっと周波数分解能を上げたい場合は、FFTへの音声データを1024から2048に増やすという点も考えられます。そうすると、2倍の21.5くらいの倍数で周波数が取得できるようになります。さらに4096だとその半分で10Hz毎くらいになります。一方で、1秒間に44100サンプル数のみなので、FFTの間隔が長くなり、更新の間隔が遅くなります。
先ほど参考にしたサイトには、4096がよく使われる、という記載が見られたように、必要な周波数の分解能と、処理速度などで、システムに合わせて数値を変更する必要があるみたいですね。
performFrequencyOnlyFowardTransformについて、JUCEフォーラムの記事も参考にしました。
https://forum.juce.com/t/fft-tutorials-issues/34957
また、ここで紹介されているFFTのドキュメントは何かと勉強になりそうです。

