リッジ回帰のパラメータによって学習曲線がどんな風に変わるか確認してみたよ
パラメータの違いを視覚化するのも大事だね
前回は、リッジ回帰のalpha=10のときの学習曲線を描きました。リッジ回帰のパラメータを変化させることによって、学習曲線にどんな変化があるのかを確認してみました。リッジ回帰は、「L2ノルム」という数値を変化させることで、重みを0に近づける方向に調整して、過学習を防ぐという効果がありました。scikit-learnのリッジ回帰では、パラメータalphaの値を大きくすることでかかり方が強くなります。
リッジ回帰のパラメータについてはこちらの記事もご参考ください。

前回の記事はこちらをご参考ください。

こんな人の役にたつかも
・機械学習プログラミングを勉強している人
・ボストン住宅価格データのリッジ回帰を勉強している人
・学習曲線を複数同時に引きたい人
・scikit-learnで学習曲線のプログラムを作成したい人
パラメータを変化させたリッジ回帰の学習曲線
リッジ回帰のパラメータを変化させて学習曲線として表示することで、パラメータ間にどのような精度の違いがあるのかなど観察できればと思いました。
今回もデータはボストン住宅価格データで、特徴量は、特徴選択を行っています。
ボストンの住宅価格データの特徴選択については、こちらの記事もご参考ください。

早速プログラムだね
まずは、importです。そして、ボストン住宅価格データを読み込んで、特徴量を絞っています。最後に、train_test_splitで75%の訓練データと、25%のテストデータに分けています。
from sklearn.datasets import load_boston
from sklearn import linear_model
from sklearn.model_selection import train_test_split
from sklearn.model_selection import learning_curve
import matplotlib.pyplot as plt
panda_box = load_boston()
X = panda_box.data
y = panda_box.target
#0:CRIM 1:ZN 2:INDUS 3:CHAS 4:NOX 5:RM 6:AGE 7:DIS 8:RAD 9:TAX 10:PTRATIO 11:B 12:LSTAT
X = X[:,[0, 1, 2, 3, 5, 8, 10, 11, 12]]
#訓練データとテストデータに分割(テストデータ25%)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25)次に、リッジ回帰のパラメータalphaが10の場合、1の場合、0の場合(0の時は線形回帰)の3つの学習曲線データを作成するために、「train_sizes1」のように変数に番号をつけて単純に三回、learning_curveを呼び出しています。
#Ridge alpha=10
train_sizes1, train_scores1, valid_scores1 = learning_curve(
linear_model.Ridge(alpha=10), X_train, y_train, train_sizes=np.linspace(0.1, 1.0, 10), cv=5)
train_score_average1 = np.mean(train_scores1, axis=1)
valid_score_average1 = np.mean(valid_scores1, axis=1)
#Ridge alpha=1
train_sizes2, train_scores2, valid_scores2 = learning_curve(
linear_model.Ridge(alpha=1), X_train, y_train, train_sizes=np.linspace(0.1, 1.0, 10), cv=5)
train_score_average2 = np.mean(train_scores2, axis=1)
valid_score_average2 = np.mean(valid_scores2, axis=1)
#LinearRegression
train_sizes3, train_scores3, valid_scores3 = learning_curve(
linear_model.Ridge(alpha=0), X_train, y_train, train_sizes=np.linspace(0.1, 1.0, 10), cv=5)
train_score_average3 = np.mean(train_scores3, axis=1)
valid_score_average3 = np.mean(valid_scores3, axis=1)
前回のプログラムのlearning_curveを三つやってるだけだね。
手抜きでは・・・ないですよ
最後に、matploylibで、3個分の学習曲線データを一つのグラフに重ねて描いています。
#図の描画
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(train_sizes1, train_score_average1, color='green' , linestyle = "solid")
ax.plot(train_sizes1, valid_score_average1, color='red' , linestyle = "solid")
ax.plot(train_sizes2, train_score_average2, color='green' , linestyle = "dashed")
ax.plot(train_sizes2, valid_score_average2, color='red' , linestyle = "dashed")
ax.plot(train_sizes3, train_score_average3, color='green' , linestyle = "dotted")
ax.plot(train_sizes3, valid_score_average3, color='red' , linestyle = "dotted")
ax.set_title("learning curve")
ax.set_xlabel("sample_size")
ax.set_ylabel("accuracy")
ax.grid(True)実線がalpha10、破線がalpha1、点線が線形回帰になります。
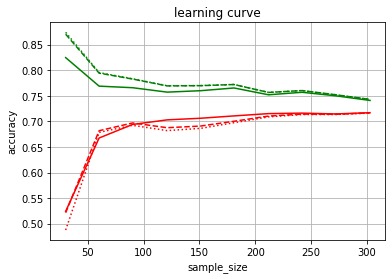
サンプル数が250以上だと、どのパラメータでもあまり変わらないね・・・
グラフからわかること
ボストンの住宅価格データへリッジ回帰を行った結果、250サンプル以上あれば、パラメータに関係なく同じような精度に収束していきます。
サンプル数が少ない時、50サンプル程度の時は、リッジ回帰パラメータが大きい方が、訓練データへの精度が低く、テストデータへの精度が高いので、過学習が抑えられていることもわかりました。
もう少し違いが欲しかったね・・・

