学習曲線というものをしりました。
アルゴリズムのチューニングに役立つね。
機械学習アルゴリズムのチューニングをするにあたって、訓練データへの精度と未知のテストデータへの精度がサンプル数においてどのように変化しているのかを知ることができる、学習曲線というものがあります。学習曲線は、アルゴリズムの学習がうまくいっているのかを評価する基準にもなります。今回は、学習曲線をscikit-learnを使って描き、リッジ回帰を評価してみようと思います。
こんな人の役に立つかも
・機械学習プログラミングの勉強をしている人
・機械学習の学習曲線について知りたい人
・scikit-learnで学習曲線を描きたい人
学習曲線をプログラミングで描く
学習曲線
学習曲線は、機械学習に訓練をさせたとき、サンプル数によってどのように精度(決定係数)が変化していっているのか、グラフにしたものです。まずは、scikit-learnのボストン価格データ、リッジ回帰のalpha=10で学習曲線を作成してみます。
学習曲線を描いてみる
まずは、importを行います。
・load_boston:ボストン住宅価格データ
・linear_model:リッジ回帰を利用
・train_test_split:とりあえず検証用データ75%と分割するために利用
・learning_curve:今回勉強した学習曲線を描くための機能
・matplotlib:学習曲線を可視化するために利用
importした後に、ボストン住宅価格データをXとyに読み込み、特徴量選択しています。
特徴量選択に関しては、以下の記事もご参考ください。

from sklearn.datasets import load_boston
from sklearn import linear_model
from sklearn.model_selection import train_test_split
from sklearn.model_selection import learning_curve
import matplotlib.pyplot as plt
panda_box = load_boston()
X = panda_box.data
y = panda_box.target
#0:CRIM 1:ZN 2:INDUS 3:CHAS 4:NOX 5:RM 6:AGE 7:DIS 8:RAD 9:TAX 10:PTRATIO 11:B 12:LSTAT
X = X[:,[0, 1, 2, 3, 5, 8, 10, 11, 12]]
#訓練データとテストデータに分割(テストデータ25%)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25)
#訓練データ個数
y_train.shape[0]訓練データ個数は、答えデータであるy_trainのshapeで確認することができます。
75%の個数の379個となりました。
今回は、train_test_splitで75%に分割する必要はなかったかも
学習曲線はパラメータのチューニングの過程で必要になるから、25%のテストデータは残しておいたほうが良いね
learning_curveというscikit-learnの機能を利用することで、サンプル数を指定した個数の場合で試して精度を出してくれます。
train_sizes, train_scores, valid_scores = learning_curve(linear_model.Ridge(alpha=10), X_train, y_train, train_sizes=np.linspace(0.1, 1.0, 10), cv=5)
①のパラメータには、リッジ回帰のモデル、訓練データ、サンプル数、交差検証分割数を設定します。ここのcvのパラメータは、交差検証の際に利用するサンプルデータの分割数になります。今回は5分割としました。
一番わかりにくかったのは、サンプル数「train_sizes」でした。ここは、配列で指定します。
「train_size=[10,50,100]」というように指定すると、10サンプル、50サンプル、100サンプルを検証してくれます。
このサンプル数は交差検証でさらに訓練データとテストデータに分割される訓練データの個数になります。
今回は、[ 30 60 90 121 151 181 212 242 272 303]のサンプル数を設定しました。これは、numpynのlinspaceという機能で作成しています。
print(np.linspace(0.1, 1.0, 10))[0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1. ]このように、0.1〜1.0までの配列ができます。learning_curveのパラメータ、train_sizesの配列に0.1と入れると、訓練データの10%としてくれるので、303の10%、30サンプル数となります。同様に、0.2、0.3・・・と10パターンのサンプル数の交差検証を行う設定とすることができます。
先ほどの割合で指定したサンプル数は、learning_curveが返してくれる値の②のtrain_sisesに入ってきます。
print(train_sizes)[ 30 60 90 121 151 181 212 242 272 303]③のtrain_scoresには、5分割交差検証の検証結果が入ってきます。printしてみましょう。
print(train_scores)[[0.76450943 0.78714126 0.78714126 0.78714126 0.78714126]
[0.76686984 0.74329504 0.74329504 0.74329504 0.74329504]
[0.74218486 0.76473234 0.7428751 0.7428751 0.7428751 ]
[0.72571954 0.73831846 0.73669518 0.73669518 0.73669518]
[0.77114609 0.77439322 0.74165074 0.74165074 0.74165074]
[0.72290093 0.72569288 0.6911192 0.73721698 0.73721698]
[0.70342709 0.71189269 0.68746105 0.74887648 0.74887648]
[0.70673771 0.71184368 0.68746793 0.75431286 0.73454417]
[0.68643403 0.69454765 0.67544321 0.72849461 0.73929648]
[0.67466849 0.68611042 0.67055584 0.71688023 0.71406803]]2次元配列の形で出力されます。
1行目がサンプル数0.1(30個)のときの5分割交差検証の訓練データに対する精度です。5分割交差検証なので、5回分の精度が配列としてみられます。
同様に2行目がサンプル数0.2(60個)のときの交差検証結果となり、10行分しっかりと存在していることが確認できました。
同じように、④のvalid_scoresについても確認してみます。
print(valid_scores)[[0.58077512 0.21897445 0.53097158 0.26280729 0.36827636]
[0.62985449 0.63996156 0.72474269 0.57348208 0.62161248]
[0.66498941 0.62019945 0.73357944 0.58000673 0.6297924 ]
[0.67294051 0.63039511 0.73217149 0.57835734 0.61333117]
[0.70068799 0.65910643 0.7457112 0.580822 0.61447942]
[0.68341512 0.66141365 0.74657924 0.58878316 0.60752649]
[0.70667861 0.68058913 0.74817309 0.58386336 0.60848871]
[0.70563176 0.68439952 0.76350318 0.58318512 0.59716322]
[0.7175305 0.68420898 0.75704204 0.58301104 0.58786135]
[0.73202771 0.68181066 0.74888899 0.57602712 0.6000616 ]]これは、交差検証を行ったときの、テストデータに対する精度になります。オレンジの部分のテストデータに対する精度ですね。
アルゴリズムから見ると、ここが未知のデータに対する精度になります。これを5分割交差検証なので、各サンプル数の検証に対して5回の検証を行っていることになります。

最後に、matplotlibを利用してグラフにしてみます。まずは、各サンプル数で5回分の結果を平均しましょう。
numpyのmeanで、axis=1とすることで、2次元配列(表)の行方向(横方向)の平均を取ることができます。train_scoresとvalid_scoresの両方平均をとります。
train_score_average = np.mean(train_scores, axis=1)
valid_score_average = np.mean(valid_scores, axis=1)matplotlibでグラフ化です。横軸がサンプル数、縦軸が精度になります。
plt.plot(train_sizes, train_score_average, color='green')
plt.plot(train_sizes, valid_score_average, color='red')
plt.title("learning curve [Boston Ridge alpha=10]")
plt.xlabel("sample_size")
plt.ylabel("accuracy")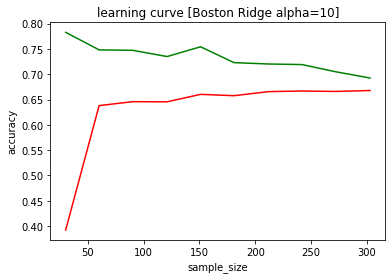
緑色のラインが、訓練データに対する精度、赤色のラインが、テストデータに対する精度です。
今回の学習曲線の評価
サンプル数が50程度までは、明らかにサンプル数不足が原因で訓練データへの精度が高いのに、テストデータへは全くダメな状態です。
サンプル数200くらいから、訓練データへの精度は少しづつ下がりますが、テストデータへの精度がほぼ横ばい(若干上昇しているように見えます)となっています。
おそらく、このボストンの住宅価格データはこの時点で、同様の特徴量のサンプル数を増やしても、リッジ回帰のalpha=10では精度向上の可能性が低いと考えられます。
サンプル数多ければ多いほど良いと思ってたけど・・・
無駄にサンプル数を集める労力をかけなくて良い判断基準にもなるね

