サポートベクターマシンがどのように動いているのかを勉強しました。
アルゴリズムの中身を少しでも理解しようとすることは大事だよね。
サポートベクターマシンはscikit-learnのライブラリで簡単に利用することができます。内部的に、サポートベクターマシンが何をして境界線を決定しているか、という点について勉強していきたいと思います。
サポートベクターマシンでアヤメのデータを分類する記事はこちらをご参照ください。

こんな人の役に立つかも
・機械学習プログラミングの勉強をしている人
・サポートベクターマシンについて勉強している人
・サポートベクターマシンのイメージをつかみたい人
サポートベクターマシン(SVM)
線形分離可能な問題とは
最も基本的なサポートベクターマシンの考え方は、「線形分離可能な2クラス問題に対応」するものです。
せんけーぶんりかのうな、にくらすもんだい

特徴量が2個のデータの場合を例にとると、上の図のように、縦軸と横軸のグラフとして可視化できます。また、このグラフには、緑の点で示したデータと、青の点で示したデータがあり、緑が答え「0」のデータ、青が答え「1」のデータを示しています。アヤメのデータでいうと、「setosa」のデータと「verginica」のデータ、のような感じです。
アヤメのデータについてわからない方は、以下の記事をご参考ください。

この図のように、答え「0」のデータと、答え「1」のデータを分類する問題が与えられたときに、両方のデータが交わらず、きれいに直線で分離できること、それが線形分離可能な2クラス問題です。
下の図はきれいに分離できません。

①線形分離可能→直線で分けられる(3特徴量の時は平面、4特徴量以上のときは超平面と呼びます)
②2クラス→分離する答えが2種類(「0」または「1」)
マージンの最大化
サポートベクターマシンは、マージン最大化という処理をすることでちょうどよいところに分類の境界線をひくことができます。
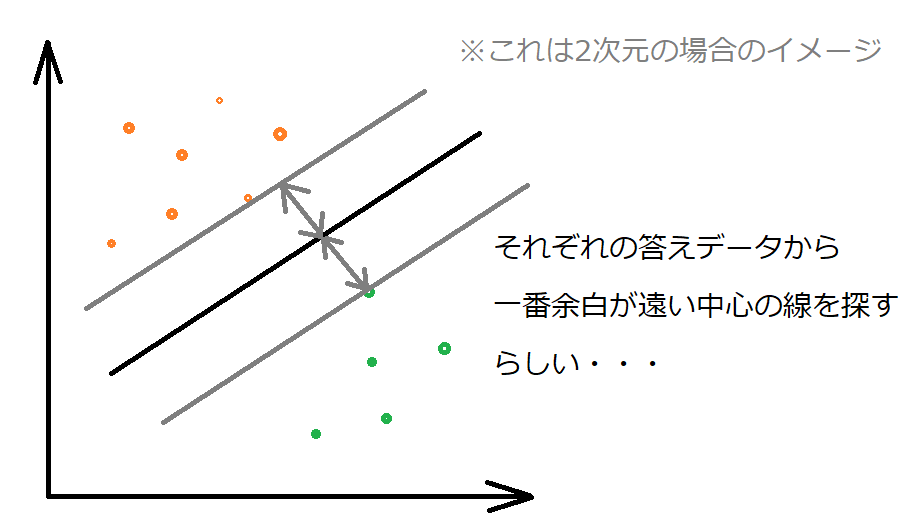
境界線から答えデータ「0」への距離、答えデータ「1」への距離が最大になるように直線の傾きを決定していきます。
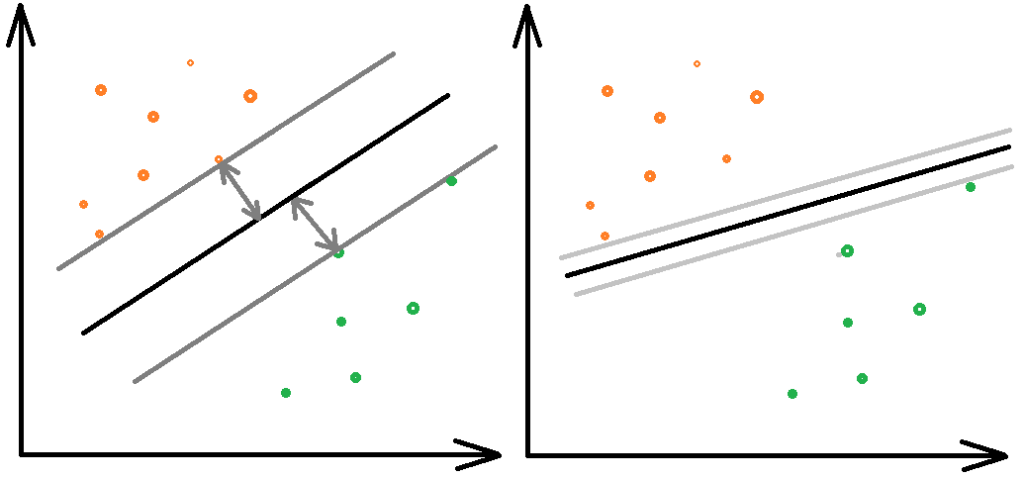
上の図の右のような境界線を引くこともできますが、マージンが最大の傾きの直線が存在するため、サポートベクターマシンではこの境界線は選択されません。
頭いいね
サポートベクトル
サポートベクトルは、マージンが最大化されたときに、マージンと接する点のことです。点が余白をサポートしているように見えます。
ハードマージンとソフトマージン
線形分離可能な問題である程度イメージができたところで、線形分離可能でない場合はどうなるの?という点が疑問になります。
実際、アヤメのデータで、線形分離できない特徴量データもあり、過去にプログラムして、分類問題に適用させてきていました。
ここで出てくるのが、ハードマージンとソフトマージンという考え方です。
ハードマージン
マージンを最大化するにあたって、マージン(余白)にデータが存在しないようにするのがハードマージンです。当たり前ですが、この場合は、線形分離可能なデータしか分離できませんよね。
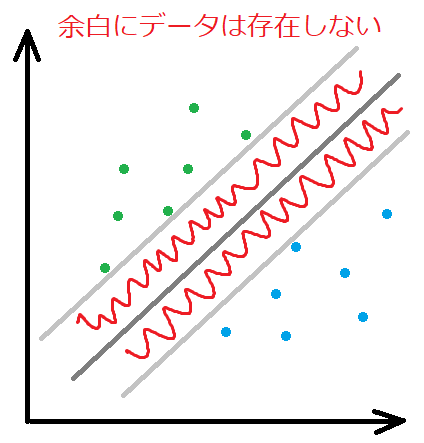
マージンに立ち入るとことは許さぬ
マージンにデータが、存在しないだと・・・
ソフトマージン
一方、ソフトマージンは、マージン(余白)の中にデータ(厳密には余白の境界より反対方向へはいったデータ)があってもOKとします。
余白の中にあるデータの距離の合計を計算してそれが最小になるような境界線を見つけることで、線形分離できないデータに対しても境界線を設けることができるようになりました。
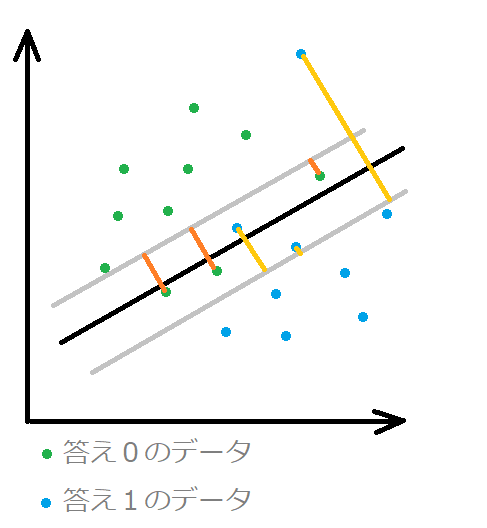
緑と青のそれぞれの答えデータが入り混じっていて、線形分離できない、上の図でいくと、緑のデータに対しては「濃いオレンジの線」の距離、青のデータに対しては「薄いオレンジの線」がそれぞれ最短になるように黒の境界線を決めていきます。
多クラス問題への拡張
サポートベクターマシンがソフトマージンの考え方で、線形分離ができないデータでも対応できるようになりました。
scikit-learnのサポートベクターマシンは、アヤメデータの分類のように、他クラス問題にも対応可能です。
これは、「one versus rest」や「one versus one」という考え方を取り入れているためです。
これは、他クラスを2クラス問題に置き換えて合わせることで他クラス問題に対応するという頭の良い方法です。
one against one はいまいち理解できていない・・・
そのうち理解できるかな・・・
以前、ロジスティック回帰のところでも「one versus rest」を紹介しました。

実際には、scikit-learnの「LinearSVC」には、「ovr」(one versus rest)が利用され、「SVC」というカーネルを使うサポートベクターマシンが「ovo」(one against one)が利用されるとのことです。
とりあえず、このようなロジックでサポートベクターマシンは他クラス問題にも対応できています。
カーネルを利用する
ここまでくると、数学的な説明もよくわからなくなってくるのですが、scikit-learnのサポートベクターマシンの「SVC」というものには、カーネルというものが指定できます。
これは、「カーネルトリック」というなんだかとても頭の良い手法を利用することで今まで直線でしか境界線を作成できなかったところが、曲線で境界を引けるようになるというものです。
カーネルは、scikit-learnの「SVC」へ与えるパラメータで指定できます。
scikit-learnを使えば、カーネルトリックという小難しい手法も簡単に使える。

