【AIプログラミング】特徴量の確認と選択、マルチコについて考える

前回の記事で、特徴量の選択は、目的変数（ボストン住宅価格データの場合価格データ）に相関が強いものを選択することを学びました。もう一つの特徴量の選択として、「多重共線性」という観点がありましたので、それについて勉強しました。

相関が強い特徴量選択については、前回の記事をご参考ください。

こんな人の役にたつかも

・機械学習プログラミングを勉強している人

・多重共線性についてふわっと知りたい人

・回帰で特徴量選択について知りたい人

多重共線性（マルチコ）に気をつける

前回の特徴量選択では、目的変数、「MEDV」の価格データ、予測したい数値に対する特徴量の相関係数を観察して、特徴量を選択しました。

今回の「多重共線性」については、説明変数同士の相関の強さをみて、特徴量を選択するという観点になります。

多重共線性は、説明変数同士の関係性（相関係数が＋１または−１に近い）が強いと、scoreで求めた値（決定係数）が高くなってしまい、本来の予測より楽観的に見積もってしまうという現象らしいです。

前回の相関係数をプロットしたものを見てみます。

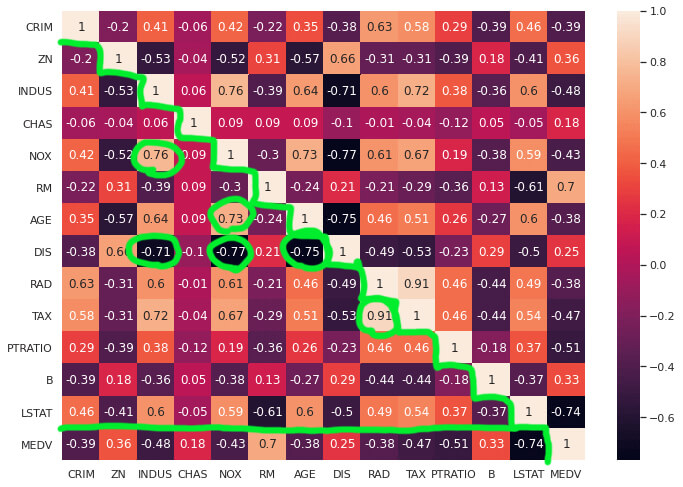
「CRIM」の行以外は、緑色の階段状の境界線よりしたを見ればデータが対になっているので、全てのデータを確認できることになります。

この組み合わせから、相関係数が-0.7以下、または0.7以上のものを緑色の丸で囲みました。

このような、特徴量同士に相関があると、予測精度に問題が発生する可能性があります。

こういった多重共線性を排除した特徴量選択を行う必要がありそうです。

特徴量を選択して多重回帰を行う

今回は、多重共線性を回避するため、上で緑色の丸をつけた特徴量を除外して多重回帰を行ってみます。

#最小二乗法による重回帰（共線性を考慮して特徴量を選択）
from sklearn.datasets import load_boston
from sklearn import linear_model
from sklearn.model_selection import train_test_split

panda_box = load_boston()

X = panda_box.data
#0:CRIM 1:ZN 2:INDUS 3:CHAS 4:NOX 5:RM 6:AGE 7:DIS 8:RAD 9:TAX 10:PTRATIO 11:B 12:LSTAT
#「RM」と「LSTAT」の列のみ選択
X = X[:,[0, 1, 2, 3, 5, 8, 10, 11, 12]]

y = panda_box.target

#訓練データとテストデータに分割(テストデータ25%)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25)

#線形回帰を作成して訓練させる
reg = linear_model.LinearRegression().fit(X_train,y_train)

print("テストデータで評価")
print("決定係数R：　{:.3f}" .format(reg.score(X_test, y_test)))

特徴量を選択するには、Pythonのスライスという配列の指定方法が有効です。

X = X[:,[0 , 1, 2, 3]]のように記載することで最初の「：」は全ての行を示し、カンマを挟んだ次の数値の配列[0,1,2,3]が、選択する列を示します。このようにして、表から必要なデータを選択することができます。

train_test_splitによって選択されるテストデータが変更になると、決定係数も変化するのですが、だいたい60％〜70%くらいの精度で未知のデータを予測することができています。

テストデータで評価
決定係数R：　0.655

この数値は、全ての特徴量で重回帰を行った時とそれほど精度が変化していませんでした。ただ、今回のような特徴量選択をすることで、次のようなメリットがあります。

・特徴量が減少するので、計算コストがへる。

・多重共線性を回避できる。

まとめ：特徴量選択について

計算コストは、ボストン住宅価格データのよりももっと特徴量が多いデータがある場合、顕著に効果があると思います。

多重共線性については、もっと深めるには数学的な部分など、ちょっと難しい点がありそうです。そのため、特徴量同士で相関が高いもの同士は除いていくという方向性で考えるのが良いと感じました。

特徴量選択は、

・目的変数と相関が強い特徴量を選択する。

・特徴量どうし相関が強いものは省くなどする。