教師あり学習の「回帰」について、回帰とはどういうものか勉強

機械学習には、種類があり、その中の教師あり学習を学んできました。教師あり学習には、「分類」と「回帰」という２種類の課題があり、今までは主に分類について学んできました。いろいろ調べてみると、回帰の中でも、特に「線形回帰」は線形モデルの基本理論的な位置づけで書かれていることが多く、この線形回帰をまず学ぶことが重要だと思いました。

機械学習の種類についてはこちらの記事をご参考ください。

こんな人の役に立つかも

・機械学習プログラミングを勉強している人

・教師あり学習の回帰についてザックリ知りたい人

教師あり学習のなかの回帰

「回帰」は英語で「regression」と呼びます。

回帰の概要

「回帰」問題は、今までみてきた「分類」問題とは違い、連続的な値を予測するものです。

例えば、現実的かどうかは別として、公務員は、年齢が上がると年収が上昇するという関係性があるとします。

この場合、「年齢」という値から「年収」を予想するモデルが作成できると考えます。

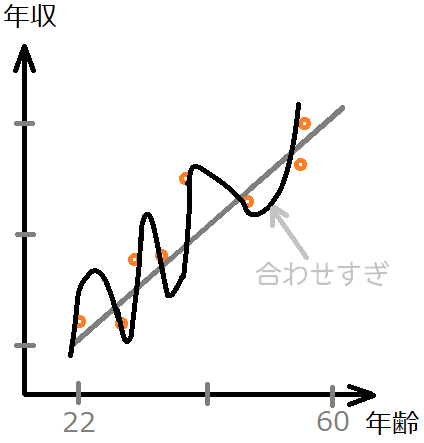
たくさんの公務員の方の年齢と年収のデータを集めたものが「オレンジの点」として、図のように分布しているとします。ここに、灰色に引いた直線のようなラインを引くことで、一般的にこの年齢ならこれくらいの年収、といった予測が可能になるはずです。

この場合は、昔、数学で勉強した

y = ax + b

という直線の式である程度予測ができそうな気がします。

この場合、yが「年収」で、xが「年齢」です。

そして、直線の傾き「a」や切片「b」を訓練によりいい感じのものを導き出してくれる、というイメージができます。

全体としてちょうど良い予測線を引く

先ほどの線は、私が目視で描いたものです。

人なら、ちょど良い線を感覚で定めることができるのですが、プログラムにさせようと思うとどのようにやったら良いでしょうか。

ここで、存在するデータから、先ほど私の能力で行った「ちょうどよい線を引く」という行為を行わせるために工夫したプログラムが、機械学習の回帰になります。

先ほどの予測する線と、個別のデータには、いくらかの誤差が生まれるのですが、この誤差に合わせすぎると「過学習」と呼ばれる現象が発生してしまいます。機械学習アルゴリズムで回帰を行わせると、過学習が起こってしまい、うまく予測が働いてくれなくなってしまう可能性がありますので、この過学習を防ぐテクニックもあります。

この過学習を防ぐために、「正則化」というテクニックが使われたりします。

このちょうど良い線を見つけるための方法には色々あります。

「直線」（や平面や超平面）で予測線を見つける「線形」な回帰の方法や、曲線（や曲面など）で予測線を見つける「非線形」な回帰の方法があります。

目的変数と説明変数

「年齢」がこの値になると、「年収」がこうなる、のように、「この値がこうなると・・・」というものを「説明変数」とよびます。また、予測される値を「目的変数」と呼びます。

目的を説明する変数

と理解するとイメージが付きやすいでしょうか？

先ほどの式

y = ax + bでは、yが目的変数、xが説明変数となります。yを予測するために「ax+b」が存在しています。

単回帰と重回帰

私たちの世界には、先ほどの例のように、「年齢」が変化すれば「年収」が決まる、みたいな単純な問題はほぼないです。

実際には、先ほどの「年齢」以外にも、「労働時間」が長いほど年収が下がる…とか、そういった多くの要因が「年収」を決定づけているはずです。

先ほどの、１つの説明変数（先の「年齢」）に対して１つの目的変数（先の「年収」）が決まるような回帰問題を、「単回帰」というそうです。

y = ax + b　は、説明変数xが一つのみです。

また、「年齢」以外の「労働時間」などのような多くの説明変数が存在するものを「重回帰」と呼ぶそうです。

実践の方向性

データを利用して、実際にどのように「回帰」のプログラムが動作するのかを見ていくことは重要です。

「ボストンの住宅価格データ」というものがscikit-learnにあります。このデータを利用して、回帰のプログラムに挑戦していきたいと考えています。

また、回帰のアルゴリズムとしては、最小二乗法を見ていき、リッジ回帰、ロッソ回帰という流れを勉強していくのが王道のような感じのようです。理解できるかは別としてそのように勉強していこうと考えています。