【AIプログラミング】scikit-learnのPCAで次元削減、サポートベクターマシンで乳がんデータを分類

前回、PCAを試してみてどんな風に特徴量を抽出するのか、なんとなくのイメージが持てました。今回も、もう少しPCAについて勉強してみました。寄与率という概念でPCAが抽出する特徴量をみていくことも重要でした。

前回のPCAを試す記事につきましては、こちらをご参考ください。

PCAで抽出した特徴量の寄与率

scikit-learnをはじめとするライブラリにはPCAを簡単にやってくれるプログラムがすでに存在しますので、データセットをPCAというプログラムに入れるだけで、主成分となる特徴量に変換してくれます。

そこで、PCAを利用する上で重要なことは、

「抽出された主成分となるデータは全てが有効な特徴量になるとは限らない」

という点です。

抽出された主成分となる特徴量には、それぞれのデータに与える影響度というものがあります。

例えば、前回のプログラムで抽出した２つの主成分はどうみてもX軸方向のデータを利用した方がY軸方向のデータよりも表現力が高いことが視覚的にもわかると思います。

「表現力が高い」と曖昧な言葉と使ってしまいましたが、これを数値で計算したものが「寄与率」というものです。

scikit-learnのPCAでは、訓練させると自動的に「explained_variance_ratio_」という部分に計算された寄与率が入ってきます。

プログラミングで実践

30個ある乳がんデータの特徴量全てをPCAして、寄与率をみてみます。

importから

まずは、importから、訓練データとテストデータにデータを分割するところです。

from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns

#ボストン住宅価格データの読み込み
panda_box = load_breast_cancer()

X = panda_box.data
y = panda_box.target

#訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, stratify=y, random_state=0)

標準化

次に、標準化を行います。

訓練データでStandardScalerをfitして、訓練データ(X_train)、テストデータ(X_test)をtransformします。この時、テストデータでfitをしてしまうと、基準がずれてしまうので、訓練データでfitしたStandardScaler(scaler)でテストデータもtransformします。

標準化につきましては、こちらの記事もご参考ください。

#標準化
from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
#訓練データをもとに標準化して訓練データを標準化
X_train_scaled = scaler.fit_transform(X_train)
print(X_train_scaled.shape)
X_test_scaled = scaler.transform(X_test)
print(X_test_scaled.shape)

PCA

次に、PCAをします。

「pca=PCA()」は、パラメータ設定デフォルトでのPCAになります。この時、抽出される主成分の数（特徴量数）は、「データ数と次元数の少ない方の主成分数が得られる」とのことです。今回は509>30なので、30次元の主成分が得られます。

X_train_scaledは標準化された訓練データですが、PCAもこの訓練データでfitします。fitしたら、transformで主成分を抽出します。

#PCA
from sklearn.decomposition import PCA

#デフォルト設定のPCA
pca = PCA()
pca.fit(X_train_scaled)
X_train_pca = pca.transform(X_train_scaled)
X_test_pca = pca.transform(X_test_scaled)

#寄与率を表示
print(pca.explained_variance_ratio_)

30個の主成分が抽出されましたので、それぞれの寄与率がPCAの「print(pca.explained_variance_ratio_」で表示できます。

[4.44812457e-01 1.89285933e-01 9.44660299e-02 6.58814275e-02
 5.27661493e-02 3.96361361e-02 2.48135833e-02 1.62011491e-02
 1.50629941e-02 1.20473636e-02 9.11056814e-03 8.14374394e-03
 6.34431822e-03 5.19738838e-03 3.48016593e-03 2.53477743e-03
 1.90283791e-03 1.81804163e-03 1.55186158e-03 1.03815503e-03
 9.16237321e-04 8.19008697e-04 6.85176925e-04 5.43258947e-04
 3.86885653e-04 2.66315467e-04 2.19574286e-04 4.28127197e-05
 2.14836222e-05 4.16485987e-06]

そして、この配列をmatplotlibでグラフにしてみます。

寄与率は、データに対する影響度の大きさのようなものなので、

plt.plot(pca.explained_variance_ratio_)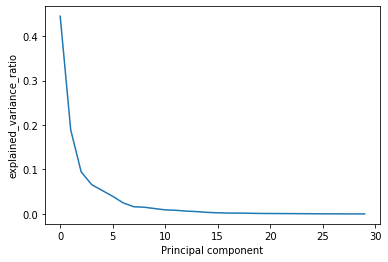

X軸は、主成分の数(0～29)あり、寄与率の大きい順に並んでいることがわかります。このグラフからわかるのは、15個目の成分からは寄与率がほぼゼロで、必要のない特徴量ということがわかります。

特徴量の削減をしてみる

試しに、30個の成分で行った訓練と、15個の成分で行った訓練の精度の違いを見てみることにします。

識別器はサポートベクターマシンで行いました。

#サポートベクターマシン
from sklearn import svm

cls = svm.SVC().fit(X_train_pca, y_train)

print("訓練データ：{:.4f}" .format(cls.score(X_train_pca,y_train)))
print("テストデータ：{:.4f}" .format(cls.score(X_test_pca,y_test)))

訓練データ：0.9930
テストデータ：0.9580

#寄与率が高い次元のみを選択

cls2 = svm.SVC().fit(X_train_pca[:,0:15], y_train)

print("訓練データ：{:.4f}" .format(cls2.score(X_train_pca[:, 0:15],y_train)))
print("テストデータ：{:.4f}" .format(cls2.score(X_test_pca[:, 0:15],y_test)))

訓練データ：0.9930
テストデータ：0.9510

30個と、15個では、訓練データに対する精度は同じで、テストデータへの精度も15個の特徴量で0.007程度低いだけです。

特徴量が少ないと、訓練するコストが少なくでき、より実用的になりますので、PCAかなり有効な手段とわかります。