主成分分析という手法を勉強しているけど、仕組みが難しいよ。
scikit-learnだと、PCAという機能に入れるだけで簡単にできるみたい。
データの標準化を学び、いい感じの結果が出たので、データを変換することを調べていました。そして、主成分分析(PCA)というデータの特徴量を変換する方法を勉強しました。仕組みが統計的な内容など、かなり高度な内容になってきているのですが、なんとか上澄みだけでも理解してscikit-learnのライブラリのPCAがどんな結果をくれて、どのように使えるのか、わかるようにしていきたいです。
データの標準化についてはこちらをご参考ください。

こんな人の役にたつかも
・機械学習プログラミングを勉強じている人
・機械学習の主成分分析(PCA)を勉強している人
・scikit-learnでPCAを利用したい人
PCAについて
PCAは日本語で、主成分分析の英語名の略称です。
与えたデータから本質的な特徴量を抽出してくれるので、「教師なし学習」に該当するアルゴリズムです。
特徴量を回転して、本質的な特徴量を抽出
お互いに相関が高い特徴量同士では、機械学習の訓練には冗長なデータとなってしまうことがあります。
例えば、オレンジの点のようなデータの2つの特徴量があり、次のように回転して変換すると、2つの特徴量から「主成分1」のような1つの本質的な特徴量が作成できます。
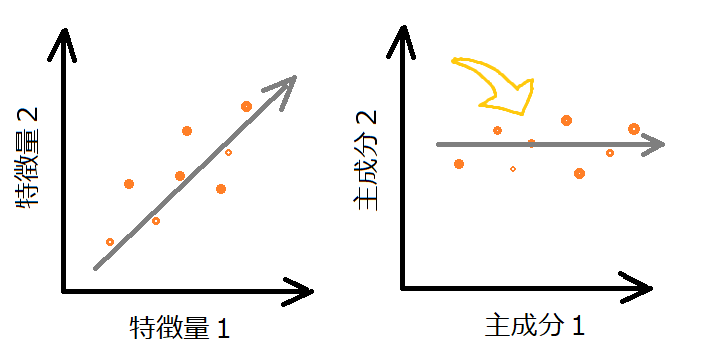
特徴量1が体重、特徴量2が身長だったら、体型というもっと抽象的な特徴量が得られるかもね。
プログラムで確認
実際に、特徴量が二個の時にPCAがどのように動作するのかを見ていきます。
from sklearn.datasets import load_breast_cancer
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
#データの読み込み
panda_box = load_breast_cancer()乳がんデータの特徴量のデータ分布を確認するため、ペアプロットします。
ペアプロット については、こちらの記事もご参考ください。

特徴量が30個あるので、4個の特徴量に限定して表示します。
#データフレームに特徴量0と特徴量2を入れる。
df = pd.DataFrame(panda_box.data[:, 0:4])
#答えデータフレームにする
target_df = pd.DataFrame(panda_box.target)
#特徴量データと答えデータのデータフレームを合体させる。
md = pd.merge(df, target_df, left_index=True, right_index=True)
md.columns = ['mean radius', 'mean texture', 'mean perimeter', 'mean area', 'target']
#シーボーンでペアプロット
sns.pairplot(md, hue="target")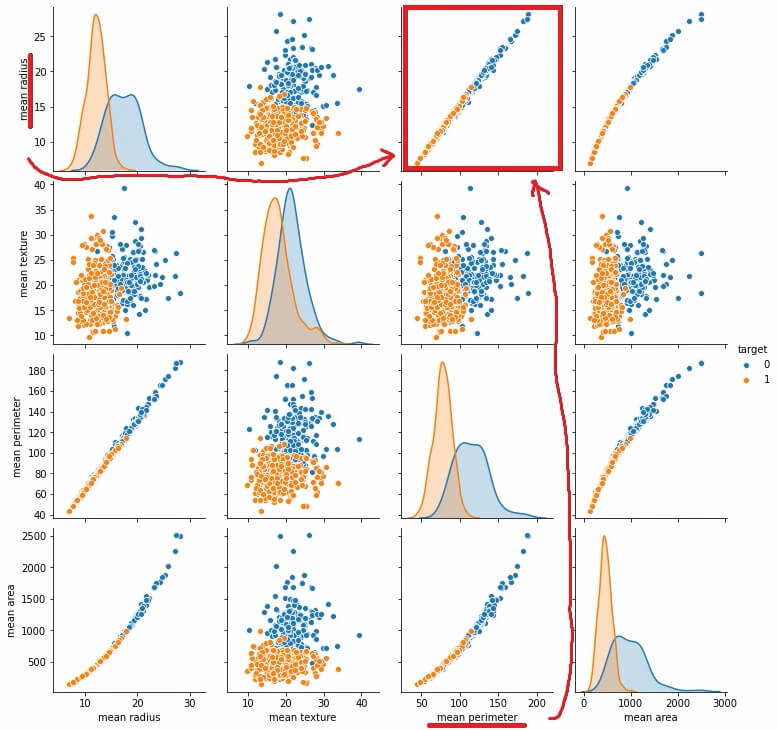
特徴量の「mean radius」と「mean perimeter」の組み合わせのグラフが直線的でPCAの変換がわかりやすそうです。PCAで特徴量の変換を行ってみたいと思います。
「mean radius」と「mean perimeter」のみのデータとして、そのグラフを描きます。
#特徴量「mean radius」と「mean perimeter」を取り出し
b_data = panda_box.data[:,[0,2]]
#取り出した後の形状を確認
print(b_data.shape)
#matplotlibでグラフの確認
fig = plt.figure(figsize = (6, 6))
ax = fig.add_subplot(111)
ax.scatter(b_data[:, 0],b_data[:, 1])
ax.set_xlabel("mean radius")
ax.set_ylabel("mean perimeter")(569, 2)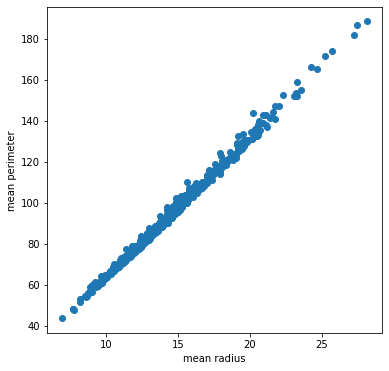
ペアプロットで描いた、先の図の赤枠の散布図と同じだね。
PCAで変換
次に、PCAをimportします。
scikit-learnではPCAを読み込み、
「作成」→「訓練(fit)」→「変換(transform)」
するだけでPCA変換処理が行えてしまいます。
from sklearn.decomposition import PCA
pca = PCA()
pca.fit(b_data)
pca_data = pca.transform(b_data)
#matplotlibでグラフを描く
fig2 = plt.figure(figsize = (6, 6))
ax2 = fig2.add_subplot(111)
ax2.scatter(pca_data[:, 0],pca_data[:, 1])
ax2.set_ylim(-40,40)
この横軸方向の特徴量はもはや最初の「mean radius」と「mean perimeter」という特徴量の軸ではない点がみそです。この特徴量は、先のプログラムのpca_dataの一列目の部分に格納されていて、「mean radius」と「mean perimeter」の性質を織り込んだようなデータとなっています。
まとめ
PCAについて、ふわっと理解できたつもりでいます・・・
PCAは内部的に面白い仕組みがありそうで、その部分も掘り下げていきたいと考えています。でも、現状はscikit-learnのPCAモジュールでできるので、他のことを優先的に勉強していきたいと思います。
次の記事にて、PCAを利用して特徴量を抽出、サポートベクターマシンにて分類問題に挑戦しています。


