【AIプログラミング】アヤメデータでクラスタリングを試す、クラスタリングの特性

アヤメデータを２次元に抽出したものにクラスタリングをしてみました。もともと答えデータが決まっているものを答えなしでクラスタリングしたらどうなるか、という興味からです。クラスタリングの特性も確認することができました。

クラスタリングの基本的な使い方についてはこちらの記事もご参考ください。

こんな人の役に立つかも

・機械学習プログラミングを勉強している人

・クラスタリングを勉強している人

・アヤメデータをクラスタリングして確認したい人

アヤメのデータで確認

まずは、importして、アヤメのデータを読み込みます。

from sklearn.datasets import load_iris
import matplotlib.pyplot as plt

import numpy as np
import pandas as pd

panda_box = load_iris()

X = panda_box.data
y = panda_box.target

グラフとして視覚化できるように、アヤメのデータの２つの特徴量「sepal length」「sepal width」のみのデータとします。ついでにシーボーンで可視化するため、データフレームにして「pd_X」に入れています。

pd_X = pd.DataFrame(X[:, 0:2])
pd_y = pd.DataFrame(y)

#表の結合
md = pd.merge(pd_X, pd_y, left_index=True, right_index=True)

#結合した表の列名をつける。
md.columns = ['sepal length', 'sepal width', 'target']
print(md)

import seaborn as sns
sns.scatterplot(data=md,x='sepal length',y='sepal width',hue='target')

シーボーンでアヤメの種類別にデータのプロットの色を変更したいので、答えデータの「target」も表として一体化します。pd.mergeで合体です。合体した表は次のようになります。

     sepal length  sepal width  target
0             5.1          3.5       0
1             4.9          3.0       0
2             4.7          3.2       0
3             4.6          3.1       0
4             5.0          3.6       0
..            ...          ...     ...
145           6.7          3.0       2
146           6.3          2.5       2
147           6.5          3.0       2
148           6.2          3.4       2
149           5.9          3.0       2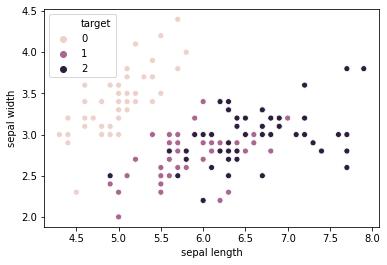

アヤメデータの「sepal length」「sepal width」では、「setosa(0)」はしっかり他の種類と分離していますが、「versicolor(1)」「virginica(2)」はデータが混ざっています。

クラスタリングでは、このようなデータはどんな風に分けられるのでしょうか、試してみたいと思います。

Kmeansに指定する「n_clusters」はもちろん３です。

from sklearn.cluster import KMeans

kmeans = KMeans(n_clusters = 3)
kmeans.fit(pd_X)

#ラベルづけされる。
print(kmeans.labels_)
pd_label = pd.DataFrame(kmeans.labels_)

[2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 0 0 0 1 0 1 0 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1
 0 0 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 0 0 1 0 0 0 0
 0 0 1 1 0 0 0 0 1 0 1 0 1 0 0 1 1 0 0 0 0 0 1 1 0 0 0 1 0 0 0 1 0 0 0 1 0
 0 1]

最初に２が並んでいますね。

#表の結合
md = pd.merge(pd_X, pd_label, left_index=True, right_index=True)
md.columns = ['sepal length', 'sepal width', 'label']

sns.scatterplot(data=md,x='sepal length',y='sepal width',hue='label')

どうやら、setosaが2となりましたが、setosaのみはうまく分類できてそうです。しかし、「versicolor」「virginica」のように混ざり合っているものはこのように分類するようですね。

kmeansは、データの重心をみて分類するのでこのような分け方になります。そして、混ざり合っているようなデータをクラス分けするのは苦手なようですね。

kmeansの仕組みについても勉強して記事に落とし込みたいと思います。