scikit-learnのボストン住宅価格データを知る

回帰問題を試すために、scikit-learnのボストンの住宅価格データというものを利用していきます。利用にあたって、まずはどのようなデータなのか、調べていきたいと思います。

こんな人の役に立つかも

・機械学習プログラミングを勉強している人

・教師あり学習の回帰について勉強している人

・scikit-learnのボストン住宅価格データについて知りたい人

ボストン住宅価格データの概要

まずはscikit-learnからボストン住宅データを読み込み、どのようなデータなのかの説明文を覗いてみます。

アヤメのデータのようにloadで読み込むことができます。ボストン住宅価格データの場合は、「load_boston」という機能で読み込むことができます。

from sklearn.datasets import load_boston
import pandas as pd

panda_box = load_boston()
print(panda_box.DESCR)

load_bostonによってscikit-learnからボストン住宅価格データを読み込んだら、このデータがどのようなものなのか説明文を表示してみます。

DESCRというところに説明文が入っているので、例のごとくpanda_box.DESCRとすることで説明文にアクセスできます。これをprint文で表示してみましょう。

.. _boston_dataset:

Boston house prices dataset
---------------------------

**Data Set Characteristics:**  

    :Number of Instances: 506 

    :Number of Attributes: 13 numeric/categorical predictive. Median Value (attribute 14) is usually the target.

    :Attribute Information (in order):
        - CRIM     per capita crime rate by town
        - ZN       proportion of residential land zoned for lots over 25,000 sq.ft.
        - INDUS    proportion of non-retail business acres per town
        - CHAS     Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
        - NOX      nitric oxides concentration (parts per 10 million)
        - RM       average number of rooms per dwelling
        - AGE      proportion of owner-occupied units built prior to 1940
        - DIS      weighted distances to five Boston employment centres
        - RAD      index of accessibility to radial highways
        - TAX      full-value property-tax rate per $10,000
        - PTRATIO  pupil-teacher ratio by town
        - B        1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
        - LSTAT    % lower status of the population
        - MEDV     Median value of owner-occupied homes in $1000's

    :Missing Attribute Values: None

    :Creator: Harrison, D. and Rubinfeld, D.L.

「Number of Instances: 506」により、506個のデータが含まれています。506戸の住宅について、データを採取したことがわかります。

「Number of Attributes: 13」により、このデータの特徴量が13個あることがわかります。そして、予測に使うデータは、データの形が数値データやカテゴリ分けによるデータ（0がこれ、1がこれみたいな数値で種類を示すようなデータ）形式になっていることがわかります。また、答えデータの住宅価格は、「Median Value」であることが表示されています。「MedianValue」は、中央値という翻訳なのですが、おそらく、住宅価格は変動するので、その中央の値で代表的な価格としてます、みたいなイメージかと思います。

その下に、13の特徴量がどのようなものかの説明文があります。

特徴量を詳しく見てみよう

単純にGoogle翻訳に入れただけですが、いくつかは直感的にわかりにくかったのと、住宅に関する知識がないので、翻訳しつつ、データの世界観を調査しました。

①CRIM：町ごとの一人当たりの犯罪率

単純に住宅が所属する地区の一人当たりの犯罪率、のようなイメージかと思います。

②ZN：25,000平方フィートを超える区画に分けられた住宅地の割合。

25000平方フィート以上の住宅部分の割合？

③INDUS：町あたりの非小売業エーカーの割合

エーカーは面積なので、住宅がある町の非小売業（カフェなどのサービス業）の割合。

④CHAS：チャールズ川ダミー変数（=河道が河川に接している場合は1、それ以外の場合は0）

ダミー変数は、数値のように連続的でないもの（接している１、それ以外０など）を数値として表現することで、住宅がチャールズ川に接しているかどうかを表現したデータです。

⑤NOX：一酸化窒素濃度（1000万分の1）

住宅の空気の測定結果ですかね。一酸化窒素濃度です。

⑥RM：住居の部屋の平均数

住宅の部屋数です。

⑦AGE：1940年より前に建てられた所有者が居住するユニットの割合

住居のどれくらいの割合が1940年より前の建造かという割合だと思います。

⑧DIS：5つのボストン雇用センターまでの加重距離

ボストンの５か所の雇用センターへの距離を加重平均とったものだと考えられます。おそらく、センターの大きさなどで加重しているのでは、と思います。

⑨RAD：放射状高速道路へのアクセシビリティのインデックス

おそらく高速道路入口のようなところへのアクセスのしやすさを数値化したものだと思います。

⑩TAX：＄10,000あたりの固定資産税率

⑪PTRATIO：町別生徒-教師比率

住宅がある町の生徒と教師の比率です。数値からして、教師１人に対して何人の生徒か、みたいな感じですね。教育が住宅価格に影響あるのか、という点が観測できそうですね。

⑫B：町ごとの黒人の比率

翻訳ではよくわからない感じになりましたので、わかる部分のみ抜粋しました。住宅の町の黒人の比率かと考えられます。。

⑬LSTAT：人口のより低いステータス

階級が低い人の人口割合ですね。低階級がどのようなものなのかは不明です。

⑭MEDV：所有者が居住する住宅の中央値（$ 1000）

住宅価格の変動を1000$を最小単位として平均化した価格のイメージかと思います。

データの取得をしてみよう

実際の住宅データ

先ほどの「MEDV」が目的変数で、予測すべき数値になります。

それ以外の特徴量がデータ説明変数となることができるものです。

①～⑬までは次のように「data」に格納されています。

print(panda_box.data)

また、この①～⑬までの特徴量の名前は、アヤメのように「feature_names」から取得することができます。

print(panda_box.feature_names)

また、「MEDV」の住宅価格データ（今回の答えとなるデータ）は、「target」から取得できます。これも、アヤメデータと同じですね。

print(panda_box.target)

分類の時のデータセットと違う点として、「target_names」というものがないことです。下の図のように、「target_names」というものが存在していません。目的変数である「MEDV」以外はないので、存在しないんですね。

分類のデータ「アヤメのデータ」については、こちらの記事をご参考ください。

１３特徴量と５０６戸住宅データを見やすく

一番最初にPandasをimportしていたのは、ここで使うためです。

「feature_names」が13特徴量のカラム名となるので、次のように指定します。

print(pd.DataFrame(panda_box.data, columns=panda_box.feature_names))

かなり画像で加工しましたが、下のようなデータがテキストで出力されるはずです。

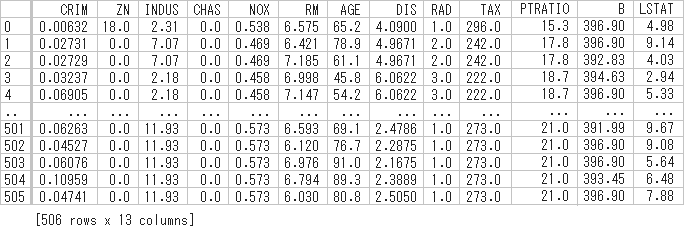
scikit-learnのボストン住宅価格データには、このように１戸あたり、１３特徴量のデータが５０６個存在しています。