ビニングなるものに出会いました。
ビニングはbinningで、特徴量をいくつかのビンに分けるんだね。
機械学習で、データ自体を色々いじって新しい特徴量を作り出したりすることを、特徴量エンジニアリングというらしです。今回は、ビニングという手法を勉強しました。ぱっと見、理解に苦しむ内容なのですが、プログラムを作成してみたら意外となるほど、と感じました。ボストンの住宅価格データの部屋数「RM」を利用して視覚化しながら勉強しました。
こんな人の役に立つかも
・機械学習プログラミングの勉強をしている人
・ビニングを勉強している人
・scikit-learnでビニングのプログラミングを勉強している人
ビニングのイメージ
線形回帰は、特徴量が1つだけだとただの直線になってしまいます。たくさんの特徴がある場合には、線形回帰はどんどんと強力になっていきますが、データによってはそうでない時もあります。
ビニングは、一つの特徴量を一定間隔のビンに分割して、それぞれの区間を違う特徴量とみなして重回帰をすることで、一つの特徴量に複雑な線を引くことができます。
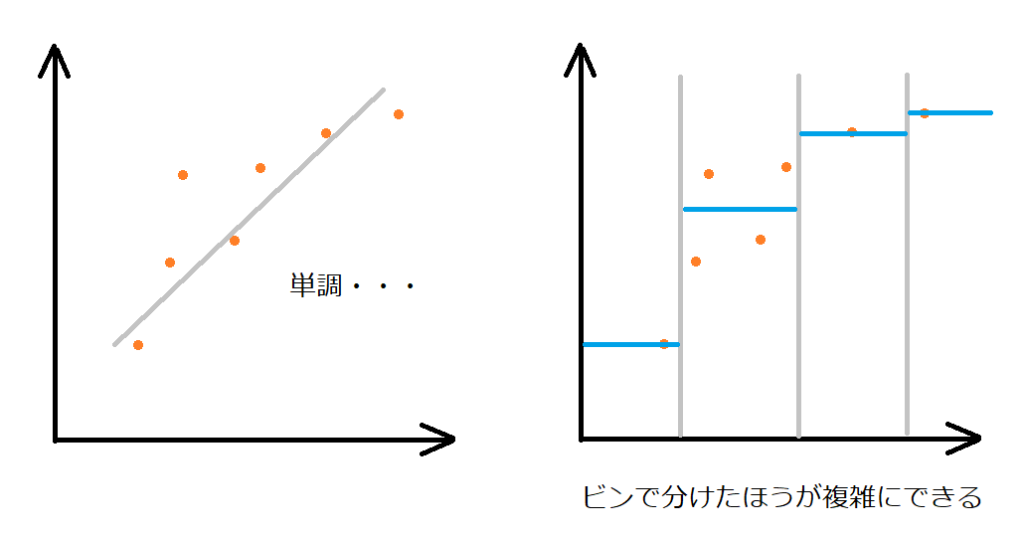
図の左は、線形回帰の単回帰になります。リッジやLassoで傾き具合をデータに適合しすぎないようにしていました。右の図が、今回やろうとしているビニングのイメージです。
ビニングは、離散化とも呼ばれるようだね。
確かに、アナログな連続的な線から、階段状のデジタルな線になっています。
単回帰のプログラムを思い出す
ボストンの住宅価格データのRMのみを利用して、単回帰を行うプログラムです。
以前の記事もご参考ください。

from sklearn.datasets import load_boston
from sklearn import linear_model
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
panda_box = load_boston()
X = panda_box.data
y = panda_box.target
#0:CRIM 1:ZN 2:INDUS 3:CHAS 4:NOX 5:RM 6:AGE 7:DIS 8:RAD 9:TAX 10:PTRATIO 11:B 12:LSTAT
X = X[:,[5]]
#訓練データとテストデータに分割(テストデータ25%)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state=0)train_test_splitのパラメータ、「random_state」を設定することで、乱数の種の数値を固定することで、毎回同じ分割ができるようにしました。(前回からの変更点)以前のプログラムでは、train_test_splitを実行するたびに違うデータ分割となってしまったのが、何回実行しても、同じ結果になりました。
#Ridge回帰を作成して訓練させる(alpha=0のため、普通の線形回帰)
reg = linear_model.Ridge(alpha=0).fit(X_train,y_train)
print("訓練データへの決定係数 :{:.3f}" .format(reg.score(X_train, y_train)))
print("テストデータへの決定係数:{:.3f}" .format(reg.score(X_test, y_test)))
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(X_train, y_train, color="green")
ax.plot(X_train, reg.predict(X_train), color='orange' , linestyle = "dotted")
ax.set_xlabel("RM")
ax.set_ylabel("MEDV")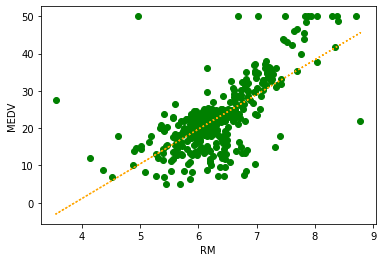
以前との違いとして、以前は、coef_とintercept_の値で愚直に計算していましたが、predictすれば普通にy軸の値がもとまるので、「ax.plot(X_train, reg.predict(X_train))」とすることで、回帰の線を描くことができるように変更しています。
オレンジの線が、線形回帰での予測線になるね。
ビニングを行う
ビニングを行う流れとして、
1.データのどこをビンとするかを決める
2.データを所属するビンの番号に変更する
3.特徴量として配列化する(ワンホットエンコーディングと呼ぶらしい)
というデータ変換を行うことで、ビニングされたデータとします。
データのどこをビンとするかを決める
numpyのlinspaceで行います。今回のRMデータは、3〜9までの範囲になるため、linspaceの範囲を3と9としました。また、今回はシンプルに見やすくするため、分割数を6としています。3〜9までの6個の分割点を得ることができます。
import numpy as np
bins = np.linspace(3,9,6)
print(bins)[3. 4.2 5.4 6.6 7.8 9. ]この分割境界の6個の数字は、ビンの範囲と対応してきます。
ビン1:「3~4.2」
ビン2:「4.2~5.4」
ビン3:「5.4~6.6」
ビン4:「6.6~7.8」
ビン5:「7.8~9」
のような範囲となります。
データを所属するビンの番号に変更する
numpyのdigitalizeで行います。これも、動作させて、どのようにデータが変化するのかを確認するとわかります。
sel_bins = np.digitize(X_train, bins=bins)
print(sel_bins.shape)
print(X_train[0])
print(sel_bins[0])X_trainの一個目のデータ(X_train[0])が5.605なので、5.4〜6.6の間に所属します。sel_binsの1個目データ(sel_bins[0])にはビン3を示す、3という数値が入ります。
(379, 1)
[5.605]
[3]全てのデータ(379個)に対してこのようにビンの番号へ変換する処理が行われます。ちなみに、この時点で、グラフ化すると、データがビン番号に変化したので、離散的なグラフになります。ここからも、離散化の意味が伝わってきます。
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(sel_bins, y_train)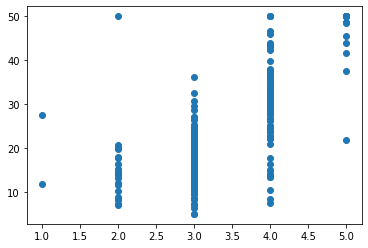
特徴量として配列化する
ワンホットエンコーディングというらしいのですが、ここも、scikit-learnのOneHotEncoderという機能で変換することができます。
ワンホットエンコーディングは、下の図のようにデータを変換します。

from sklearn.preprocessing import OneHotEncoder
encoder = OneHotEncoder(sparse=False)
encoder.fit(sel_bins)
bin_data = encoder.transform(sel_bins)
#ワンホットエンコーディングの3行目まで確認してみる
bin_data[:3]sklearnのpreprocessingから、OneHotEncoderをimportします。
そして、エンコーダ作成後、エンコーダーに先ほどのビン番号に変換したデータ「sel_bins」を入れて訓練(fit)させます。
最後に、訓練させたencorderに、「sel_bins」を入れて「transform」させることで、「bin_data」という変数に、先ほどのようなワンホットエンコーディングの形式の配列が得られます。
array([[0., 0., 1., 0., 0.],
[0., 0., 1., 0., 0.],
[0., 0., 0., 1., 0.]])線形モデルを学習させる
最後の訓練は、このビン毎に分割したデータを学習させます。これは、ビン数分のカテゴリ変数の(0または1で決定する特徴量)特徴量を訓練させるのに似ていると思います。
#リッジ回帰(線形回帰)で訓練
reg = linear_model.Ridge(alpha=0).fit(bin_data, y_train)lineという変数に、X軸方向の数値、3〜9を1000分割した数値の配列を作成しておきます。reshapeで二次元配列の形に変換しておきます。
line_binnedには、ワンホットエンコーディングに変換したline変数を入れておきます。
line = np.linspace(3,9,1000,endpoint=False).reshape(-1,1)
line_binned = encoder.transform(np.digitize(line, bins=bins))
#print(line_binned)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(X_train, y_train, color="green")
#Xに3~9の1000分割した数値、Yに訓練させたモデルにXを3~9の1000分の1づつ増加した時の値を計算させる。
ax.plot(line, reg.predict(line_binned), color='orange' , linestyle = "solid")
ax.vlines(bins, 0, 50, alpha=0.4)
ax.set_xlabel("RM")
ax.set_ylabel("MEDV")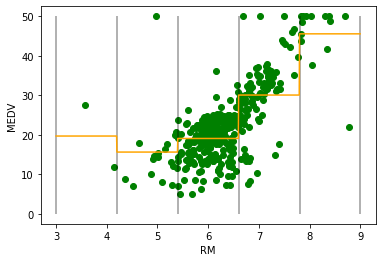
グラフを描く時、少しややこしかったのが、
「ax.plot(line, reg.predict(line_binned), color=’orange’ , linestyle = “solid”)」のところです。
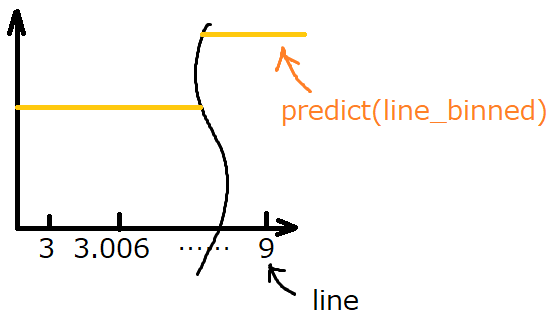
predictでy軸をプロットするのですが、lineデータをビン化したものを入れます。そうすることで、lineの配列(正確には2次元配列)の全ての数値に対してYの値が出せます。
スコアを比較してみる
まずは、普通の線形回帰です。
normal_reg = linear_model.Ridge(alpha=0).fit(X_train, y_train)
print("通常データの精度")
print(normal_reg.score(X_test,y_test))通常データの精度
0.4679000543136782次に、ビニングしたものの精度です。テストデータも訓練データ同様、ワンホットエンコーディング形式にしないと、モデルがデータを受け付けません。
print("5分割したビニングの精度")
#テストデータもビニング
#データをビンの番号に変換
sel_bins_test = np.digitize(X_test, bins=bins)
#ホットエンコーディング化
encoder_test = OneHotEncoder(sparse=False)
encoder.fit(sel_bins_test)
bin_data_test = encoder.transform(sel_bins_test)
#テストデータをビンにしたもので精度を評価
print(reg.score(bin_data_test,y_test))5分割したビニングの精度
0.4778030179010067若干精度が上昇しているようです。ビンの数を増やせば、このRMの特徴量に対しては、もっと複雑なモデルを作成することができそうです。
ビニングの分割数を増やすとどうなるか試してみようかな。
ビニングの処理をひとまとめに関数化できないかな?
いつかやってみよう。
ビニングの続きの記事はこちらもご参考ください。


