ニューラルネットワークの勾配について色々と考えてみました。
勾配について知ることでニューラルネットワークの理解が深まるね。
ニューラルネットワークを勉強すると、勾配、誤差関数、最適化手法といろいろな概念がでてきます。中でも、「勾配」の正体を理解することで、これらの関係性がより理解できると考え、「勾配」について私なりに考察してみました。
こんな人の役にたつかも
・機械学習プログラミングを勉強している人
・勾配についてよくわからない人
・ニューラルネットワークの勉強をしている人
シンプルな例
次のようなシンプルな直線の式があるとします。
この式の意味として、「x1の特徴データにw1という係数をかけ合わせるとtargetの数値が予測できますよ」という意味だと思ってください。
target = w1 × x1
w1:は重みといって、求めたいパラメータになります。
x1:は実データです。
target:x1の時の答えです。
この関係式のw1を求める
「x1」の値と「target」の値があれば、w1の「重み」が計算ができるので、例えば次のようにx1が「2」、targetが「5」という数値がわかった場合、w1は簡単に導くことができます。
data = [2,5]
x1 = data[0]
target = data[1] dataは配列にする必要はないのですが、雰囲気を出してみました。
w1を求めるには「w1 = target ÷ x1」なので、
「w1 = 5 ÷ 2」とすればよいです。
w1 = target/x1
print(w1)2.5ということで、w1は2.5で「target = 2.5 * x1」という関係式が導き出せました。
答えの値(target)の「5」を代入しないやり方ではどのように求めるでしょうか?
力技で「w1」を算出する
色々な値をw1とx1に代入してみて近づくように値を入れていけば、いつかtargetが5になる時がきそうです。
まずはw1に2を、x1に2を入れてみました。
w1 = 2
x1 = 2
predict = w1 * x1
print(predict)4答えは4と、欲しい値の5より小さかったので、もう少し「w1」を増やしてみます。
次はw1に3、x1に2を入れてみます。
w1 = 3
x1 = 2
predict = w1 * x1
print(predict)6w1を増やしすぎたので、少しさげてみましょう
w1 = 2.5
x1 = 2
predict = w1 * x1
print(predict)5.0w1は2.5だとtargetが5になるような関係式になることがわかりました。
w1を何回も試行して求めることもできました。
ただ、シンプルな式でない場合、ひとつづつ値を入れていくのは現実的ではないです。
総当たりをしない場合、どのようにw1を求めると良いでしょうか・・・
過去の頭の良い人たちは、正解との誤差を利用してみようと考えました。
誤差を定義する
「w1」が「2」のとき、先ほど計算したように、
2×2=4
w1 = 2
x1 = 2
predict = w1 * x1
print(predict)4となります。「w1」を「2」としたときの、とりあえずの答え「4」を本当の正解「5」との誤差を計算してみます。
誤差は英語で「error」というので変数名は「error」としました。
error = predict - target
print(error)-1「w1」を「2」とした計算式(モデル)の回答である「4」は正解の「5」から「-1」の誤差値があることになります。
この誤差の式である「error」が最小となるように予測値predictを調整していく、w1をerrorが0の方向に調整していくと、正解に近づいていくことがわかります。
ちょっと式を整理してみます。
error = predict – target
error = (w1 * x1) – target
今回の具体的な数値を入れた場合:error = (w1 * 2) – 5
「error」を最小化する操作をするためには、頭の良い人が、 「誤差を二乗にして微分すればよい」と教えてくれました。
なぜ誤差を二乗するのか??については、符号にマイナスがつくよりも、符号がすべてプラスの方がどれくらい誤差があるかわかりやすいので、二乗にします、と理解する程度で大丈夫そうです。大人の事情で絶対値は利用しないとのことでした。
また、二乗の計算とすることで、次にグラフに描くように、二次関数として表現でき、w1がいくつの時に誤差が一番小さくなるかが「微分」計算で求めることができるようになります。
ここで、「二乗誤差」というものが生まれました。
二乗は英語でsquareなので、二乗誤差をsquare_errorとします。
square_error = error * error
print(square_error)1また、この二乗誤差を微分してみます。
一度、二乗誤差の式を「w1」が見えるように整理してみます。
square_error = error × error
square_error = {(w1 * x1) – target} × {(w1 * x1) – target}
square_error = {(w1 * x1) – target}^2
※^2は二乗という意味です。念のため^^;
ここに、今回の「x1=2」と「target=5」を入れてみると
square_error = 4(w1)^2 -20(w1) + 25
という式が出てきます。
===計算詳細===
square_error = ((2 × w1) – 5)^2
square_error = (2 × w1)^2 – (2 × 2 × w1 × 5) + (-5)^2
square_error = 4 × w1 – 20 × w1 + 25
====
上のような二乗誤差は、w1を変化させると次のようなグラフになります。
import matplotlib.pyplot as plt
import numpy as np
#二乗誤差のグラフ
w1_axis = np.linspace(0, 10, 20)
plt.xlabel("w1")
plt.ylabel("error")
plt.plot(w1_axis, w1_axis*w1_axis*4 - 20*w1_axis + 25)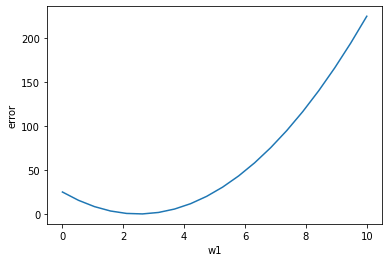
勾配が最小になるところは二次関数の微分値が0になる部分なので「接線の傾きが0になるところ」と読み替えることができます。
この「square_error = 4(w1)^2 – 20(w1) + 25」を微分します。
微分した二乗誤差を「square_error‘」と表現してみます。←左上に「’」をつけました。
微分すると
square_error’ = 8(w1) – 20 ←これが「勾配」
となることがわかります。※微分公式で微分しました。
matplotlibで視覚化するとこんな感じです。
#二乗誤差の微分「勾配」のグラフ
w1_axis = np.linspace(-5, 10, 30)
plt.xlabel("w1")
plt.ylabel("gradient(error_diff)")
plt.plot(w1_axis, 8*w1_axis - 20)
plt.plot(w1_axis, 0*w1_axis)
#図の矢印は後から付け足しました。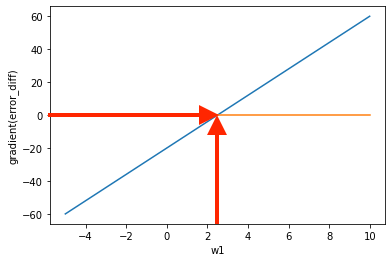
縦軸の「微分された二乗誤差」が 一般的なニューラルネットワークの「勾配(gradient)」にあたるものです。
今回は、勾配が「0」になるw1の値が、与えられたデータにおける最適な重みとなります。(x1=2,target=5以外データはないため)
勾配を「0」にするということは、「8(w1) – 20 = 0」を解くことになります。
w1 = 20/8なので
w1 = 20/8
print(w1)2.5いちいち簡単な計算もプログラムでやりたいんです、すみません。
このような操作で「w1」を求めることができました。
これが、「誤差関数を最小化にすることで重みを最適化する」という内容になります。
※誤差について、今回は回帰問題で一般的な二乗誤差を例にしましたが、そのほかにも、誤差を定義する方法があります。分類問題では一般的に「交差エントロピー誤差」という誤差を利用したりします。
より適した方向にw1を動かす「勾配降下法」
今回の場合は、1つのデータ「x1 = 2, target = 5」に合わせるようにw1を計算しましたので、「勾配が0になる点のw1」が答えとなりました。しかし実際のところ、データはたくさんあり、そのデータの集合に対してもっとも「いい感じ」のw1を見つけるのがニューラルネットの課題です。
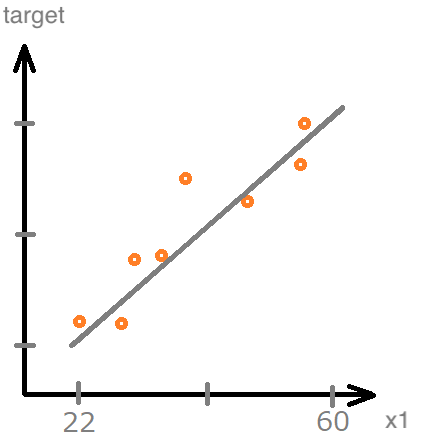
このような場合いくつものデータを通る直線というものは考えられないので、代入する方法だといつまでたってもw1がフラフラと動いて最後に試したデータのw1になってしまうことがわかります。(単純パーセプトロンの重み計算はこの考え方に近いです。)
一方、勾配を求める方法は工夫することで、全てのデータを考慮した「w1」を考えることができます。
先ほどw1を算出したときには、「x1=2、target=5」に対してのみ「w1」を合わせればよかったので、勾配が0になる点で完全なw1となりました。しかし、多くのデータが与えられたとき、そのデータの傾向によりフィットする「w1」を求めることになります。
ということは、
「w1をより多くのデータにフィットする方向に動かしてあげる」
ことが重要になってきます。
この動かし方が、「勾配降下法」と呼ばれる方法になります。
勾配降下法のまとめ方が雑だね・・・
今日は勾配までの考察で、すみません・・・
もう少し全体的にニューラルネットワークの構成要素を説明した記事として、こちらの記事もご参考ください。



