PCAに白色化なるものがあるらしい・・・
毛染めみたいな名前だね。
以前、特徴量を整える時に、教師なし学習であるPCA(主成分分析)を勉強しました。そのPCAに、白色化というものがあることがわかりました。PCAの白色化をプログラムで試して、どのように動作しているのかをみてみました。
PCAについては、以前のこちらの記事もご参考ください。

こんな人の役に立つかも
・機械学習プログラミングを勉強している人
・PCAについて勉強している人
・PCAの白色化について知りたい人
PCAの白色化
PCAの白色化について
白色化とは、相関を薄める、という意味合いで利用されているみたいです。
通常のPCAをすると、データの散らばり具合(分散)が強い方へ軸を回転させることで、データの本質的な特徴量を得られるのですが、相関が強い場合、分散が少ない方の軸の特徴量と分散が大きい特徴量の差が開いてしまいます。
以前のPCAの記事で紹介した図では、特徴量1の方が分散が大きく、そちら方向へ回転することで、主成分1というものが得られました。
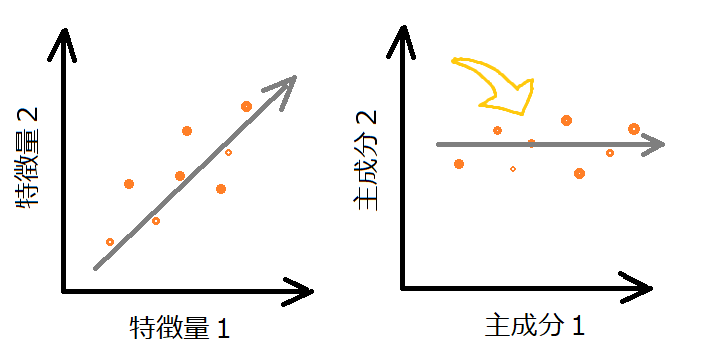
主成分2の方の特徴量データのばらつきは、主成分1のものよりもかなり小さなものとなっています。
ここに、白色化という処理を施すことで、データの散らばり具合のスケール感を整えて、相関を低くした主成分1と主成分2を作成することができます。
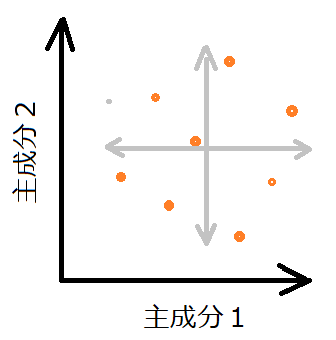
PCAの白色化を視覚的に観察
乳がんデータのimportから
まずは、scikit-learnの乳がんデータをimportします。
以前、乳がんデータでPCAを行った時は、相関の強い特徴量をPCAしていました。今回も、乳がんデータから「mean radius」と「mean perimeter」の特徴量を例としてプログラムでみていきます。
from sklearn.datasets import load_breast_cancer
import matplotlib.pyplot as plt
import pandas as pd
#乳がんデータ
panda_box = load_breast_cancer()
#グラフに描いてみる
b_data = panda_box.data[:,[0,2]]
print(b_data.shape)
#matplotlibでのグラフ描画
fig = plt.figure(figsize = (6, 6))
ax = fig.add_subplot(111)
ax.scatter(b_data[:, 0],b_data[:, 1])
ax.set_xlabel("mean radius")
ax.set_ylabel("mean perimeter")乳がんデータから「mean radius」と「mean perimeter」はグラフからも、かなりの相関がありそうです。右上に一直線です。
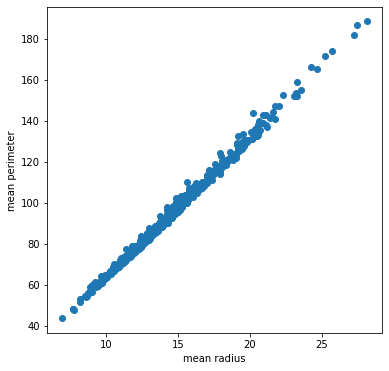
相関係数を求めてみよう
pythonで相関係数を求める方法はいくつか存在するみたいですが、pandasのseriesに変換して求める方法で計算してみます。
#相関係数を求めるための準備
def change_series(data_list):
reshaped_data = data_list.reshape(1,-1)
series = pd.Series(reshaped_data[0])
return series
series1 = change_series(panda_box.data[:, [0]])
#print(series1)
series2 = change_series(panda_box.data[:, [2]])
#print(series2)def change_seriesという関数にて、与えたデータをpandasのseries という形に変換できるようにしました。
series1で「mean radius」のデータを、series2にて「mean perimeter」のデータを入れています。
そして、相関係数を求める時は、seriesの機能「corr」にて計算します。
#相関係数を求める
soukan = series1.corr(series2)
print("相関係数")
print(soukan)見ため同様、かなり高い「正の相関」があります。
※1に近いほど正の相関、−1に近いほど負の相関、0に近いほど相関がない。
相関係数
0.9978552814938105バリバリ癒着してますな。
PCAの白色化を行います
PCAの白色化は、scikit-learnで非常に簡単に実現できます。
PCAの「whiten」パラメータを「True」にするだけです。
from sklearn.decomposition import PCA
pca = PCA(whiten=True)
pca.fit(b_data)
#pca白色化された特徴量
pca_data = pca.transform(b_data)
#matplotlibにてグラフの表示
fig2 = plt.figure(figsize = (6, 6))
ax2 = fig2.add_subplot(111)
ax2.scatter(pca_data[:, 0],pca_data[:, 1])
ax2.set_ylim(-5,5)
ax2.set_xlabel("pca_feature1")
ax2.set_ylabel("pca_feature2")pca_data変数に、PCA白色化された主成分データが入ってきますので、これをグラフ化して表示しています。
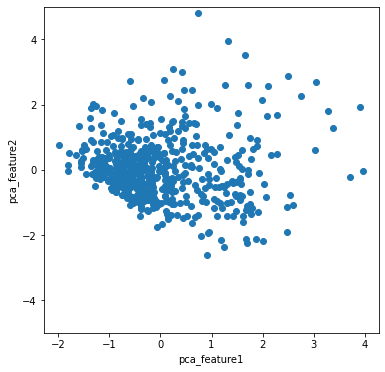
PCAだけとはちがい、かなりばらつきのあるグラフとなりました。主成分1と主成分2の相関係数も求めてみたいと思います。
pca_series1 = change_series(pca_data[:, [0]])
pca_series2 = change_series(pca_data[:, [1]])
#相関係数を求める
pca_soukan = pca_series1.corr(pca_series2)
print("PCA白色化後の相関係数")
print(pca_soukan)PCA白色化後の相関係数
4.289555799765409e-15e-15(10の-10乗)という表記の通り、かなり0に近い値になりました。このことからも、主成分1と主成分2にはかなり相関がないことがわかります。
PCAの白色化を行う方が良いかどうかは、データによるのかと思うんですが、このような方法もあるんだと心にとめておきたいと思います。

