最小二乗法って、1800年くらいとかに考案されたんだね・・・
歴史あるよね。高校でも習ったような気がするね。
前回、ボストンの住宅価格データの「部屋数」から「住宅価格」を求める時にLinearRegression(線形回帰)という方法で関係性を直線の予測線にしました。この時、最小二乗法という数学の手法を利用してちょうどいい感じの直線をひいていました。最小二乗法について、少し勉強しましたので、そのまとめです。
こんな人の役に立つかも
・機械学習プログラミングを勉強している人
・scikit-learnのLinearRegressionが何をしているのか知りたい人
最小二乗法のを勉強してみる
最小二乗法のイメージ
最小二乗法は、「実際のデータ値」と「ちょうど良い直線の差」を一番小さなものにしようとする方法です。

「ちょうど良い直線」はまだないけど・・・差の取りようがないよね??
実際に試そうとすると、全てのちょうど良さそうな直線を引いて、そのデータとの差が一番小さくなるようにするというのをまず考えると思います。まずはaの値を0.1から徐々に増やしていって・・・、次にbの値を増やしていって・・・というような感じでしょうか。
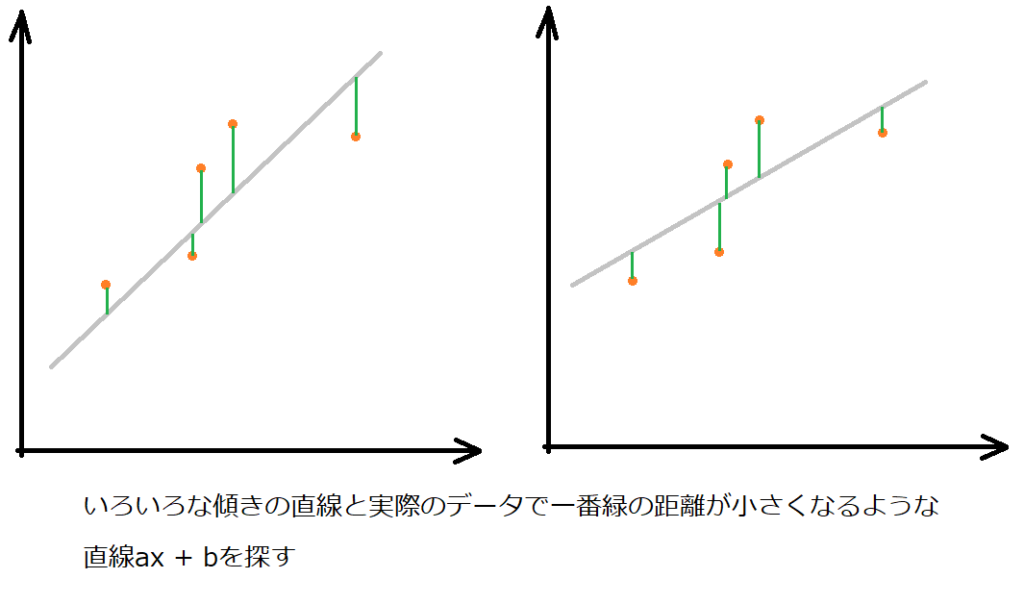
プログラムでたくさん計算させればいけそうだけど、それだとただの力技だね。
最小二乗法を使うと、公式だけで実際のデータとの差が一番小さくなるようなになるような傾きと切片が求められるよ。
ここで、最小二乗法という数学のテクを利用すると、今あるデータを元に、最適な直線の「傾き」と「切片」を導き出してくれます。
公式は、wikipediaの「一次方程式の場合」のaとbの求め方となります。
プログラムでやってみよう
プログラムとしても簡単なものなので、最小二乗法のアルゴリズムを組んでみたいと思います。
まずはボストンの住宅価格データをimportして読み込みます。部屋数「RM」の特徴量データを「X」に、住宅価格データ「MEDV」の答えデータを「y」に入れます。
from sklearn.datasets import load_boston
import numpy as np
panda_box = load_boston()
#RMのみのデータとする
X = panda_box.data[:,5]
y = panda_box.targetデータの総数(506という数値)をyの住宅価格データから取得しました。shapeの[0]番目にはデータの行数、データ個数が入っています。
data_num = y.shape[0]
print(data_num)
#傾きa
#===分子の部分===
#Xとyの積の合計(内積と同じ意味)
Xy_sum = np.dot(X,y) * data_num
#yの合計とXの合計の積
Xy_n = X.sum()*y.sum()
#===分母===
Bunbo = data_num * (X**2).sum() - X.sum()**2
#===傾きを計算===
a = (Xy_sum - Xy_n)/Bunbo
#傾き
print(a)Xとyの積の総和は、内積で求められますので、numpyのdotを使っています。
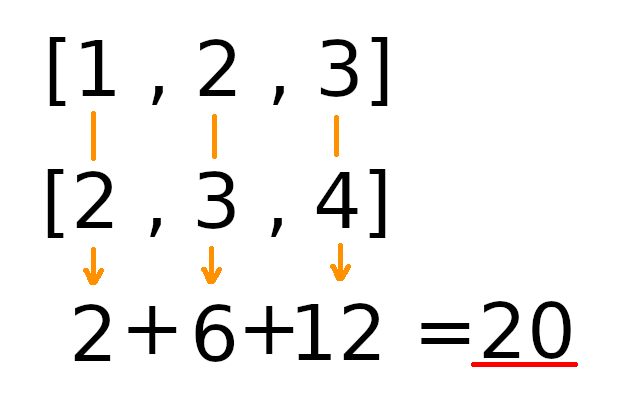
また、「Xの二乗の総和」はPythonでは「(X**2).sum()」とかくことでできいます。
↓傾きaはこのようになりました。
9.102108981180377切片bも同様に、wikipediaの数式に当てはめて計算すると、
#切片b
b = ((X**2).sum()*y.sum() - np.dot(X,y)*X.sum())/(data_num * (X**2).sum() - X.sum()**2)
print(b) -34.67062077643882このような結果になりました。
前回のscikit-learnでLinearRegressionをした時の「corf_」と「intercept_」の値と比較すると、同じ結果となっていることがわかります。
↓前回のscikit-learnによるLinearRegressionの結果(上の値がcoef_下の値がintercept_)
[[9.10210898]]
[-34.67062078]前回の記事もご参考ください。

機械学習での最小二乗法について感じたこと
機械学習プログラミングを学び始めた時は、今まで検討もしていないようなことをしてAIが作られている、と考えていました。
特に、ディープラーニングという言葉を聞くとなんかすごいことしてそうな感じが出ているので、まさか機械学習の分野で最小二乗法が出てくるとは思いませんでした。今まで学んだアルゴリズムにしても、高校数学レベルの理論で成り立っているアルゴリズムが多いイメージです。(それを証明するとなると大変なのですが・・・^^;)
実際に使う分には、「公式」と、「こんな感じのことをしているよ」といった知識が一番必要かなと感じています。そして、パラメータ調整を何回もして、うまく動くことを目指す、というのが機械学習プログラミングにおいてはまず必要な力だと思いました。
数学などの理論は、重要ですが、勉強する順番としては少し後でもいいと考えています。パラメータ調整で迷ったら深掘りして、原因を追求していく、という流れが良いのではないでしょうか。数学的に難しい実装はライブラリを作成している頭の良い方々の仕事として、利用する側は何に利用したら世の中の役に立つ機能になるかを考えることも重要だと思いました。


