前回、ロジスティック回帰で2クラスの分類をしたので、今回は3クラス分類をしてみるよ。
だんだん小難しくなってきたね。
前回は、ロジスティック回帰の2クラス問題の境界線を確認しました。今回は、one versus restという用語を勉強して、3クラスのアヤメデータの境界線を引くプログラムをうごかしてみました。
前回の記事はこちらからどうぞ

こんな人の役に立つかも
・機械学習プログラミングの勉強をしている人
・scikit-learnでロジスティック回帰の分類プログラムを勉強している人
・ロジスティック回帰の3クラス分類の境界線を引くプログラムを作りたい人
線形分類アルゴリズム、3クラス以上の分類
ロジスティック回帰は、データの境界線を直線で求めるもので、
「基本的に、2クラスのデータの境界線を引く」
ことしかできませんでした。
確かに、直線で3個に分けるの、イメージできないね
そこで、多クラス(答えが3以上ある場合)に拡張するため、「One versus rest」という考え方が使われていることを学びました。
ということで、3クラス以上あるデータは、One versus restという考え方で分類できます。
アヤメデータを分類するプログラム
前回同様、importからアヤメデータの読み込みが以下のプログラムです。
#ロジスティック回帰
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
import numpy as np
import matplotlib.pyplot as plt
panda_box = load_iris()
X = panda_box.data
y = panda_box.target
X_2dim = panda_box.data[:,:2]境界線を描く関数を作成します。
境界線を描くプログラムについては、こちらもご参考ください。

#関数を作成
def make_meshgrid(x, y, h=.02):
x_min, x_max = x.min() - 1, x.max() + 1
y_min, y_max = y.min() - 1, y.max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
return xx, yy
def plot_contours(ax, clf, xx, yy, **params):
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx, yy, Z, **params)
return out
def graf_setting(ax):
#ax.set_xticks(())
#ax.set_yticks(())
ax.set_xlabel('Sepal length')
ax.set_ylabel('Sepal width')3クラス(「setosa」「verginica」「versicolor」の3個の答え)のアヤメデータをロジスティック回帰で分類するプログラムです。
#3クラス
#===ロジスティック回帰の作成===
#訓練
clf = LogisticRegression().fit(X_2dim, y)
#空のグラフを作成
fig = plt.figure(figsize=(9, 4))
ax = fig.add_subplot(121)
#グリッドのデータを作成
X0, X1 = X_2dim[:, 0], X_2dim[:, 1]
xx, yy = make_meshgrid(X0, X1)
#グラフに境界線とデータをプロット
plot_contours(ax, clf, xx, yy, cmap=plt.cm.coolwarm, alpha=0.8)
ax.scatter(X0, X1, c=y, cmap=plt.cm.coolwarm, s=20, edgecolors='k')
graf_setting(ax)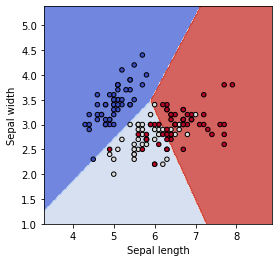
このように、ロジスティック回帰で3クラスの分類ができました。
OVR(One Versus Rest)について
本来、直線で境界線を引くということは、2クラスにしかデータを分離できないはずなのですが、3クラス以上のデータを分類する際にはOne versus restという考え方を利用することで、分類できるそうです。
ワン バーサス レスト・・・
one versus restという考え方では、「一つ」対「残り」で比較していく方法です。
例えば、アヤメの3クラスのデータは、次のように3種類の直線による境界線を引くことができます。
①「setosa」VS「verginica と versicolor」
②「verginica」VS「setosa と versicolor」
③「versicolor」VS「setosa と verginica」
というデータの比較を行います。
①のsetosaの境界線は図のようになります。
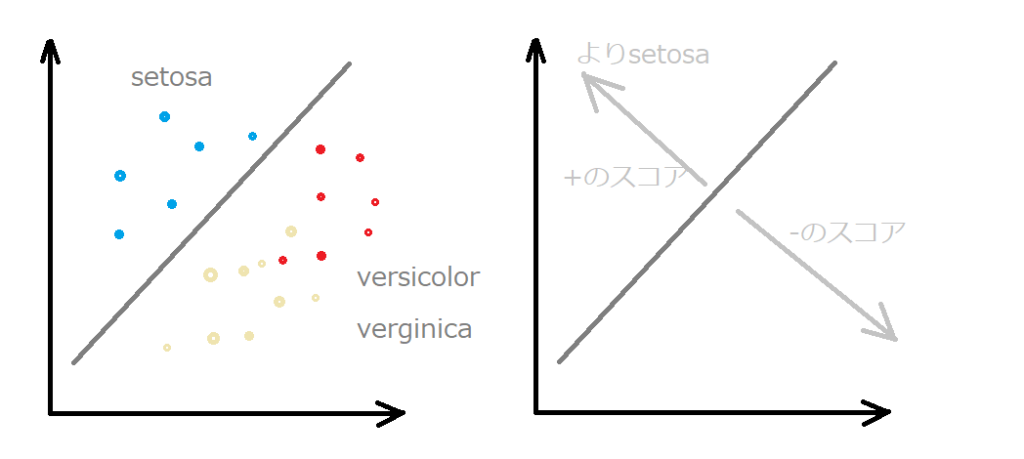
境界線の数値を0として、setosaの方向に行くほど+のスコアが高くなり、反対方向ほど、-のスコアとなるような境界線が作成されます。
①~③のそれぞれの境界線を0として、境界線同士が重なる領域には、スコアの大きい数値を採用することで、それぞれの領域を決定しています。
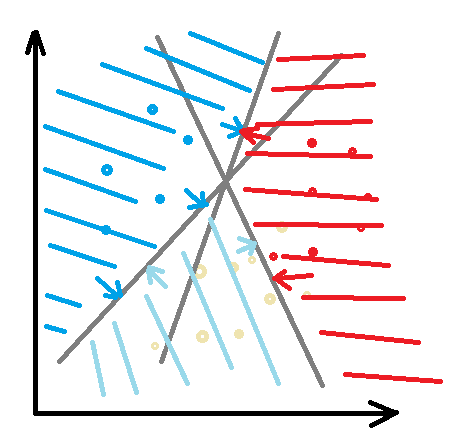
プログラムで境界線を書いてみたい・・・できなかったので、簡単なイメージ図ですみません。
数学的にもわかるといいよね。

