ロジスティック回帰は、回帰という名前がついているけれど、分類するためのアルゴリズムらしい。
ロジスティック回帰は線形に分類するためのアルゴリズムだね。scikit-learnですぐに使えるみたい。
教師あり学習の分類問題では、データの境界線をいかに定めていくか、という点が重要になります。まずは直線でその境界線を定めていく、ロジスティック回帰というものをプログラミングし、境界線を確認してみることにしました。
こんな人の役に立つかも
・機械学習プログラミングを勉強している人
・ロジスティック回帰で分類をしたい人
・scikit-learnでロジスティック回帰を利用したい人
線形に分類するアルゴリズム
機械学習の教師あり学習では、「線形の分類」というものが基本になってきます。線形に分類するアルゴリズムはいくつかありますが、その中でも基本的なアルゴリズムがロジスティック回帰です。
線形って、何??
線形は、直線
線形に分類する、とは、境界線が直線になる、ということです。

線形に分離するためのscikit-learnのアルゴリズムとしては、他に
・パーセプトロン
・線形サポートベクターマシン
などが存在しています。
2次元の特徴量では、線形に分類するとその境界線は「直線」となります。
直線は、3次元では平面に
3次元に拡張したとき、2次元の時に直線だったものは、平面となります。
3次元まではイメージできると思いますが、4次元以上でも、このように線形に分類することができます。この時、2次元で直線、3次元では平面、4次元以上だと超平面と呼ぶらしいです。
線形に分類する方法は、特徴量が少ないと、うまく分類できそうに見えませんが、特徴量が多いほど強力な分類が可能となります。
すごく雑な説明になってしまいましたが、線形、という意味のイメージができましたので、まずは2次元で、どんな境界線になるのか、見てみたいと思います。
ロジスティック回帰をscikit learnでプログラミング
アヤメのデータを2特徴量(2次元化)「sepal width」と「sepal length」のみにしたものを分類してみます。2特徴量にする理由としては、グラフで視覚化ができるからです。

まずは、ロジスティック回帰をscikit-learnからインポートします。そして、アヤメのデータを読み込み、2次元化したアヤメデータも作成しておきます。
#ロジスティック回帰
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
import numpy as np
import matplotlib.pyplot as plt
panda_box = load_iris()
X = panda_box.data
y = panda_box.target
X_2dim = panda_box.data[:,:2]次に、ロジスティック回帰の作成した境界線を視覚化するための関数を準備しておきます。これは、以前理解するために記事にしておりますので、詳細は以下の記事をご参照ください。

#境界線を視覚化するための関数たち
def make_meshgrid(x, y, h=.02):
x_min, x_max = x.min() - 1, x.max() + 1
y_min, y_max = y.min() - 1, y.max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
return xx, yy
def plot_contours(ax, clf, xx, yy, **params):
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx, yy, Z, **params)
return out
def graf_setting(ax):
#ax.set_xticks(())
#ax.set_yticks(())
ax.set_xlabel('Sepal length')
ax.set_ylabel('Sepal width')これで、ロジスティック回帰の境界線を確認するための準備ができました。
2クラス問題での分類
まずは、2クラス(答えが「setosa」または「verginica」」)となるデータを分類してみます。そのため、2クラス化したアヤメデータ(X_2dim_2clsとy_2cls)を作成しました。
最後に、matplotlibで散布図として視覚化しています。
#2クラス(「setosa」と「versinica」のみ)のデータを作成
X_2dim_2cls = X_2dim[y!=2]
y_2cls = y[y!=2]
#matplotlibで散布図を描く
fig = plt.figure(figsize=(9, 4))
fig.add_subplot(121)
plt.scatter(X_2dim_2cls[:50,0], X_2dim_2cls[:50,1], c="red")
plt.scatter(X_2dim_2cls[51:,0], X_2dim_2cls[51:,1], c="blue")
plt.xlabel('sepal length (cm)')
plt.ylabel('sepal width (cm)')
plt.grid(True)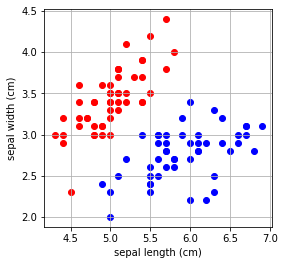
次に、このデータをロジスティック回帰で分類します。
#2クラス
#===ロジスティック回帰の作成===
#訓練
clf = LogisticRegression().fit(X_2dim_2cls, y_2cls)
#空のグラフを作成
fig = plt.figure(figsize=(9, 4))
ax = fig.add_subplot(121)
#グリッドのデータを作成
X0, X1 = X_2dim_2cls[:, 0], X_2dim_2cls[:, 1]
xx, yy = make_meshgrid(X0, X1)
#グラフに境界線とデータをプロット
plot_contours(ax, clf, xx, yy, cmap=plt.cm.coolwarm, alpha=0.8)
ax.scatter(X0, X1, c=y_2cls, cmap=plt.cm.coolwarm, s=20, edgecolors='k')
graf_setting(ax)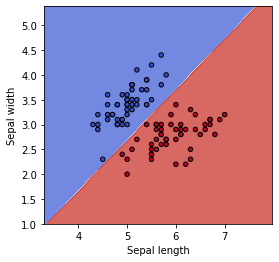
きれいに「setosa」と「vericolor」のデータを直線で分類することができました。

