コーサケンショー??アヤメのデータの分割をしていた時は、ホールドアウトという方法を使っていたね。
今までは、ホールドアウトという方法でデータを分割していたけれど、もう少しデータを満遍なく使える検証方法を勉強してみよう。
こんな人の役にたつかも
・交差検証について知りたい人
・Pythonで機械学習プログラミングを学んでいる人
交差検証について
交差検証は「CrossValidation」と呼ばれることもある。
クロスバリデーション、かっこいいからこっちを使おう。
交差検証は、汎化性能評価の安定的な方法
汎化性能の評価って、未知のデータに対する正解率なので、正直、イメージがつかないんだよね。まだ知らないことへの正解率ってなんだかおかしいよね??それをより安定的にするってことは、どんなイメージなのかな??
そうだね、プログラムからみて、知らないデータ(テストデータ)を見せて、「これくらいの正解率が出る予定だ」ということを計測する、と考えるといいかもね。
今まで何気なく使ってきた、「未知のデータに対する正解率」は、知らないデータのことを言っているようなので言葉として理解し難い部分があります。
これは、今手持ちのデータの一部をプログラムから隠しておいて、未知のデータ(テストデータ)とします。残りの訓練データを訓練することでどれだけプログラムが知らないデータに対して正解できるか?を計測します。なので、手持ちのデータの範囲内のお話になります。
結果として、私が明日摘んだ150個アヤメのデータに対してはなんの保証もないということになります。
そのため、「だいたいこれくらいの正解率で分類してくれるだろう」、という意味が「未知のデータに対する正解率」に含まれていることになります。
ホールドアウト法(scikit-learnのtrain_test_splitで分ける方法)は、単純にデータをシャッフルして、それを一定の割合で分割する、もちろんその時に答えとなるデータの偏りが内容に分割する方法でした。

ホールドアウト法と交差検証
ホールドアウトは、一度のみの分割で、そのデータはランダムにシャッフルされるという感じでした。
ということは、1回だけホールドアウトで分割した検証は、偶然性が含まれた結果が出てくることになります。
シャッフル結果によって、訓練データとテストデータの組み合わせが毎回変わるので、もしかしたらその訓練データと、テストデータの相性が抜群によかった、という場合があるわけで、その逆もあるわけです。
これを回避するために、以前のアヤメのデータ分類で、私は10回や、50回ホールドアウトを繰り返した結果の平均を「未知のデータに対する正解率」としていました。ただ、このやり方はなんとなく一回だから不安なので何回もやって平均すればいいのでは、という考えでやっていました。この点を体系的に行ってくれるのが、交差検証でした。
交差検証の内容
3分割の場合の交差検証というもので内容の説明を行います。
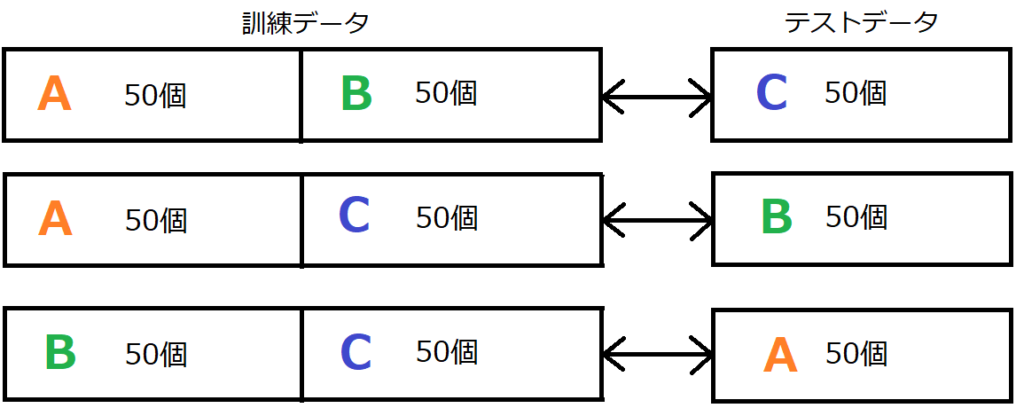
150個のアヤメのデータを3分割します。そして、それぞれをA、B、Cと呼ぶことにします。

検証する際に、訓練データとテストデータをA、B、Cの組み合わせで検証を行います。
交差検証をやってみる
今回は、k再近傍法を採用します。importして、アヤメのデータを読み込みます。そして、k再近傍法が利用できるように変数kncにk再近傍法を準備します。
from sklearn.datasets import load_iris
#交差検証のimport
from sklearn.model_selection import cross_val_score
#k-最近傍法のimport
from sklearn.neighbors import KNeighborsClassifier
import numpy as np
panda_box = load_iris()
X = panda_box.data
y = panda_box.target
knc = KNeighborsClassifier(n_neighbors = 9)次に、交差検証を行います。交差検証は、cross_val_scoreという機能で行うことができます。ホールドアウトと違うところは、このcross_val_scoreに必要な情報を与えてしまえば、自動的に検証結果を返してくれる点です。プログラムで意図的に訓練させたりする必要がないです。
#交差検証を行う。
score = cross_val_score(knc, X, y, cv=3)
#結果の表示
print("交差検証の結果")
print(score)
print("交差検証の平均")
print("{:.4f}".format(np.mean(score)))
cross_val_scoreの「アルゴリズム」の部分には、今回はk最近傍法のkncを入れます。アヤメデータはXです。答えデータはyになります。そして、分割数は「cv=」として指定します。今回は3分割で交差検証を行うので、3としました。
↓が結果です。
交差検証の結果
[0.96 1. 0.96]
交差検証の平均
0.9733クロスバリデーションすると、全部のデータが訓練データとして使われるから、ホールドアウトみたいに何回も実行させて検証っていうようにしなくてもだいたいの汎化性能がわかりそうだ・・・
交差検証については、こちらの記事もご参考ください。


