torchaudioのチュートリアル、pytorchで音声を扱う2

前回に引き続き、torchaudioのチュートリアルで勉強しています。今回は、音声データを変換する機能について出てきたのですが、変換する先のフォーマットも知っていないと何をしているのかわからなくなります^^;色々と調べながらチュートリアルを進めています。

torchaudioの１回目のチュートリアルの記事はこちらです。

こんな人の役に立つかも

・機械学習プログラミングをしている人

・torchaudioを使いたい人

・機械学習で音声を扱いたい人

音声の変換

torchaudioには、音声を変換するたくさんの機能があります。

全ての音声変換の機能は、

で確認することができます。

チュートリアルでは、「リサンプル」と「スペクトログラム」、「メル・スペクトログラム」へと変換を行います。

スペクトログラム

スペクトログラムは3次元のグラフで、縦軸に周波数、横軸に時間、色として信号の強さをとるようなものです。

specgram = torchaudio.transforms.Spectrogram()(waveform)

print("Shape of spectrogram: {}".format(specgram.size()))

plt.figure()
plt.imshow(specgram.log2()[0,:,:].numpy(), cmap='gray')

Shape of spectrogram: torch.Size([2, 201, 1324])
<matplotlib.image.AxesImage at 0x7fe38c4a5588>

スペクトログラムは、声紋などの解析に用いられます。スペクトログラムの画像をたくさん集めれば声紋判定などの訓練もできそうな予感がします。

メルスペクトログラム

スペクトログラムをより人間の耳に近い聞こえ方に修正したものがメルスペクトログラムというものらしいです。低周波数の方が高周波数よりも聞き分けやすいとのことから、低周波数の分解能をあげて、高周波数の分解能を低くするようなメルスケールというものでスペクトログラムに変換したものです。

specgram = torchaudio.transforms.MelSpectrogram()(waveform)

print("Shape of spectrogram: {}".format(specgram.size()))

plt.figure()
p = plt.imshow(specgram.log2()[0,:,:].detach().numpy(), cmap='gray')

Shape of spectrogram: torch.Size([2, 128, 1324])

リサンプル

リサンプルは、サンプリングレートを変換できます。画像では、学習用のためにサイズを小さくして情報量を減少させたりしていましたが、音声でいうとこのリサンプルがそれに相当しそうなイメージです。

そして、ステレオの２チャンネル音声から、モノラルの１チャンネル音声へと変換も行なっています。

new_sample_rate = sample_rate/10
print(new_sample_rate)

# Since Resample applies to a single channel, we resample first channel here
channel = 0
transformed = torchaudio.transforms.Resample(sample_rate, new_sample_rate)(waveform[channel,:].view(1,-1))

print("Shape of transformed waveform: {}".format(transformed.size()))

plt.figure()
plt.plot(transformed[0,:].numpy())

4410.0
Shape of transformed waveform: torch.Size([1, 26460])
[<matplotlib.lines.Line2D at 0x7fe38bd64a20>]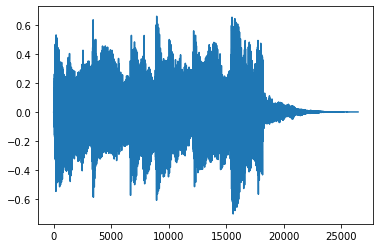

1チャンネルかつ、横軸（時間）に対するデータ量も「26460」と10分の１になっています。

音声の変換について、もう一つの例を見てみます。

「μLowエンコーディング」に基づく信号に変換することもできます。この変換を行うときは、信号が-1〜1の間になければいけません。

まずは、信号の最大値と最小値を調べて、信号が-1~1の間にあるかを調べてみます。

# Let's check if the tensor is in the interval [-1,1]
print("Min of waveform: {}\nMax of waveform: {}\nMean of waveform: {}".format(waveform.min(), waveform.max(), waveform.mean()))

Min of waveform: -0.988525390625
Max of waveform: 0.804107666015625
Mean of waveform: -1.839133801695425e-05

音声の波形がすでに-1〜1であれば、「Normalize」処理を施す必要はありません。Normalizeをする場合、次のようにNormalize関数を作成してNormalizeを行います。

def normalize(tensor):
    # Subtract the mean, and scale to the interval [-1,1]
    tensor_minusmean = tensor - tensor.mean()
    return tensor_minusmean/tensor_minusmean.abs().max()

# Let's normalize to the full interval [-1,1]
waveform = normalize(waveform)

print("Min of waveform: {}\nMax of waveform: {}\nMean of waveform: {}".format(waveform.min(), waveform.max(), waveform.mean()))

私の作成した音声では、Normalizeの必要がなかったので、上記プログラムは実行していません。

μLowエンコーディングへ変換してみます。

transformed = torchaudio.transforms.MuLawEncoding()(waveform)

print("Shape of transformed waveform: {}".format(transformed.size()))

plt.figure()
plt.plot(transformed[0,:].numpy())

Shape of transformed waveform: torch.Size([2, 264600])
[<matplotlib.lines.Line2D at 0x7f3abbcf1e80>]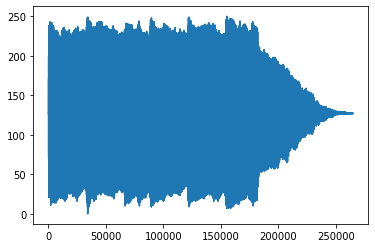

μLowエンコーディングを元に戻すデコード処理を行います。

reconstructed = torchaudio.transforms.MuLawDecoding()(transformed)

print("Shape of recovered waveform: {}".format(reconstructed.size()))

plt.figure()
plt.plot(reconstructed[0,:].numpy())

Shape of recovered waveform: torch.Size([2, 264600])
[<matplotlib.lines.Line2D at 0x7f3b27eec588>]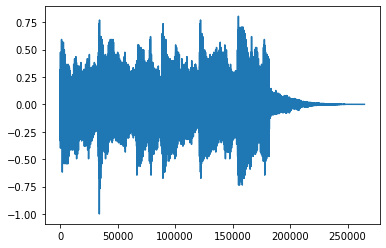

# Compute median relative difference
err = ((waveform-reconstructed).abs() / waveform.abs()).median()

print("Median relative difference between original and MuLaw reconstucted signals: {:.2%}".format(err))

今回感じたこと

いくつか音声の変換処理を見てきましたが、なんとなく機械学習へ音声データを入れるために利用するのかな、という予想ができる程度の内容となりました。リサンプルなどは、画像でもそうであったように、あまりにもデータが多すぎても学習のコストが多くなるだけなので、リサンプルして特徴が残る程度に荒くしてあげることは有効なのかな、とも考えています。他にも、音響の専門的な知識が出てきていますので、随時調べて知識を増やしていきたいです。

続きの記事はこちらです。