【AIプログラミング】KMeansのクラスタ数の妥当性を評価する、シルエット分析

教師なし学習のクラスタリングアルゴリズムのKmeansを試してきました。何気なくアルゴリズムがどんなふうに動作しているか、プログラムを動作させて確認してきましたが、そもそも何個のクラスターに分類するかは実際わからないのが前提でした。そこで、シルエット分析というものでクラスターの分類数が妥当なのかを確認することができるようです。scikit-learnの公式ページに、シルエット分析についてのドキュメントがありましたので、こちらを読んでみました。

Kmeansアルゴリズムのクラスタリングについては、こちらの記事もご参考ください。

シルエット分析について

シルエット分析をすると、

「クラスター分けが妥当なのか？」

を視覚的に確認できるようです。

シルエット分析では、次のような図を使って視覚化します。右の散布図は、どのようにクラスターに分けられたかを確認することができるようになっています。

このグラフの場合は０〜３の４つのクラスターに分類した時のグラフです。

（２特徴量に絞ったアヤメデータを４クラスターに分割してみました。）

横軸の「-0.1〜1.0」の数値は「シルエット係数」というものを表しています。

そして、クラスターの中のデータの数によってそれぞれのクラスターの帯太さが決まってきます。

そして、たての赤の点線は、全データのシルエット係数の平均を示しています。この赤線に一部が引っかかっていないクラスターがある場合、そのクラスター数は適切でない可能性がある、と見るようです。

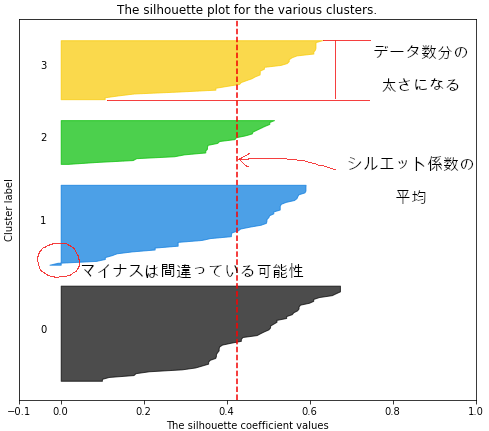
シルエット係数

＋１に近いほど、そのクラスターが隣接他のクラスターから離れているので、分離感があるクラスターということになります。

また、０に近いほどクラスターの境界線に近く、マイナスに行くと、このデータは間違ったクラスターになっている可能性があることを示すとのことです。

シルエット係数のグラフを描くプログラム

scikit-learnの公式に記載のあるシルエット分析の可視化プログラムを少し改造（ほぼコピペ・・・）してみました。

シルエット分析の可視化関数

具体的には、「def silhouette_2dim(X, range_n_clusters)」と、可視化する部分を関数化しました。Google ColaboやJupyterにて以下のプログラムブロックを実行しておけば、silhouette_2dimを呼び出すことで２次元のデータをシルエット分析することができます。

silhouette_2dim(二次元のデータ,試したいクラスター数の配列）とすることで呼び出すことができます。

#import部分
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np

def silhouette_2dim(X, range_n_clusters):

  for n_clusters in range_n_clusters:
      fig, (ax1, ax2) = plt.subplots(1, 2)
      fig.set_size_inches(18, 7)

      ax1.set_xlim([-0.1, 1])
      ax1.set_ylim([0, len(X) + (n_clusters + 1) * 10])

      clusterer = KMeans(n_clusters=n_clusters, random_state=10)
      cluster_labels = clusterer.fit_predict(X)

      silhouette_avg = silhouette_score(X, cluster_labels)
      print("For n_clusters =", n_clusters,
            "The average silhouette_score is :", silhouette_avg)

      sample_silhouette_values = silhouette_samples(X, cluster_labels)

      y_lower = 10
      for i in range(n_clusters):
          ith_cluster_silhouette_values = \
              sample_silhouette_values[cluster_labels == i]

          ith_cluster_silhouette_values.sort()

          size_cluster_i = ith_cluster_silhouette_values.shape[0]
          y_upper = y_lower + size_cluster_i

          color = cm.nipy_spectral(float(i) / n_clusters)
          ax1.fill_betweenx(np.arange(y_lower, y_upper),
                            0, ith_cluster_silhouette_values,
                            facecolor=color, edgecolor=color, alpha=0.7)

          ax1.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
          y_lower = y_upper + 10  # 10 for the 0 samples

      ax1.set_title("The silhouette plot for the various clusters.")
      ax1.set_xlabel("The silhouette coefficient values")
      ax1.set_ylabel("Cluster label")

      ax1.axvline(x=silhouette_avg, color="red", linestyle="--")

      ax1.set_yticks([])  # Clear the yaxis labels / ticks
      ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])

      colors = cm.nipy_spectral(cluster_labels.astype(float) / n_clusters)
      ax2.scatter(X[:, 0], X[:, 1], marker='.', s=30, lw=0, alpha=0.7,
                  c=colors, edgecolor='k')

      centers = clusterer.cluster_centers_
      ax2.scatter(centers[:, 0], centers[:, 1], marker='o',
                  c="white", alpha=1, s=200, edgecolor='k')

      for i, c in enumerate(centers):
          ax2.scatter(c[0], c[1], marker='$%d$' % i, alpha=1,
                      s=50, edgecolor='k')

      ax2.set_title("The visualization of the clustered data.")
      ax2.set_xlabel("Feature space for the 1st feature")
      ax2.set_ylabel("Feature space for the 2nd feature")

      plt.suptitle(("Silhouette analysis for KMeans clustering on sample data "
                    "with n_clusters = %d" % n_clusters),
                  fontsize=14, fontweight='bold')

  plt.show()

シルエット分析を試してみる

試しにアヤメデータをシルエット分析してみます。

#アヤメデータの読み込み
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt

import numpy as np
import pandas as pd

panda_box = load_iris()

X = panda_box.data
y = panda_box.target

読み込んだXの特徴量２次元分のみを抽出してXに入れ直します。

シルエット分析で可視化したいクラスター数を配列として指定します。ここでは、2クラスター〜6クラスターの場合を指定しました。

#パラメータの入力ブロック
#2次元のデータをXに指定すれば色々なデータをシルエット分析できます。
X = X[:, 0:2]

#ここに検証したいクラスター数をリストとして用意
range_n_clusters = [2, 3, 4, 5, 6]

先ほど関数化したシルエット分析の可視化関数を呼び出します。

silhouette_2dim(X, cluster_array)

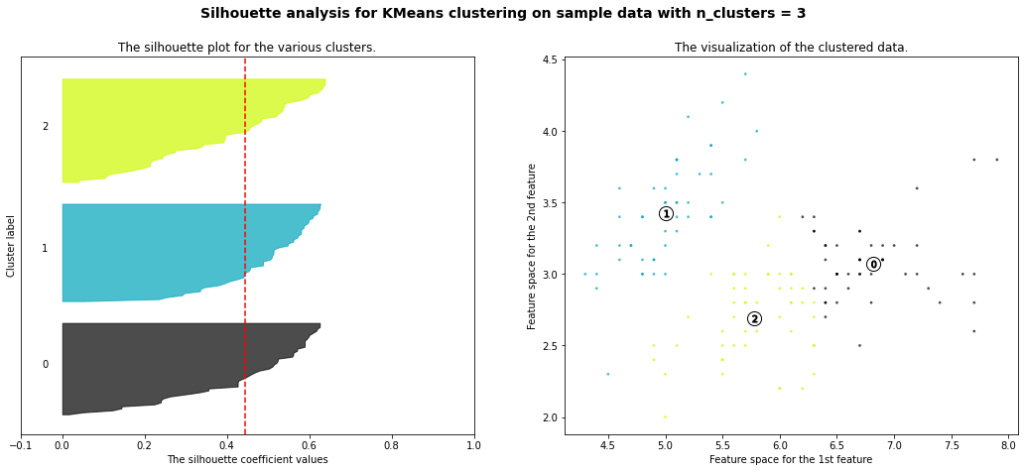
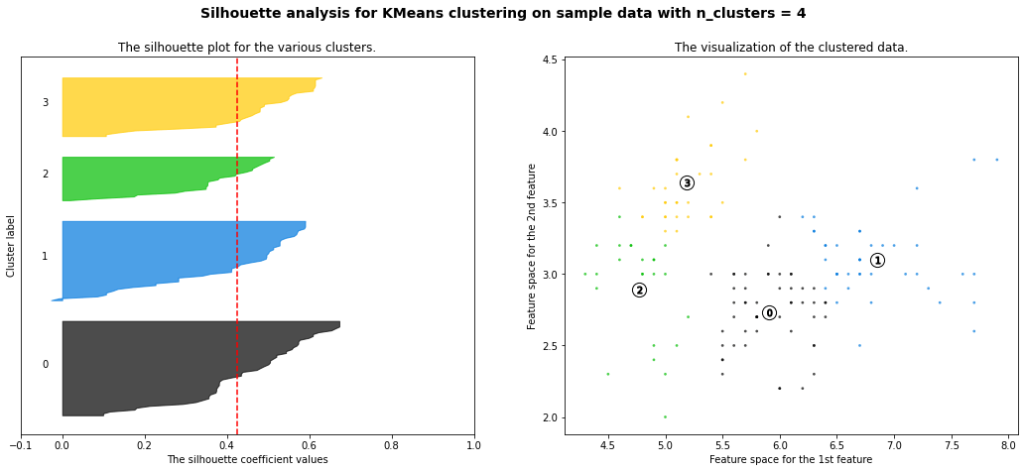
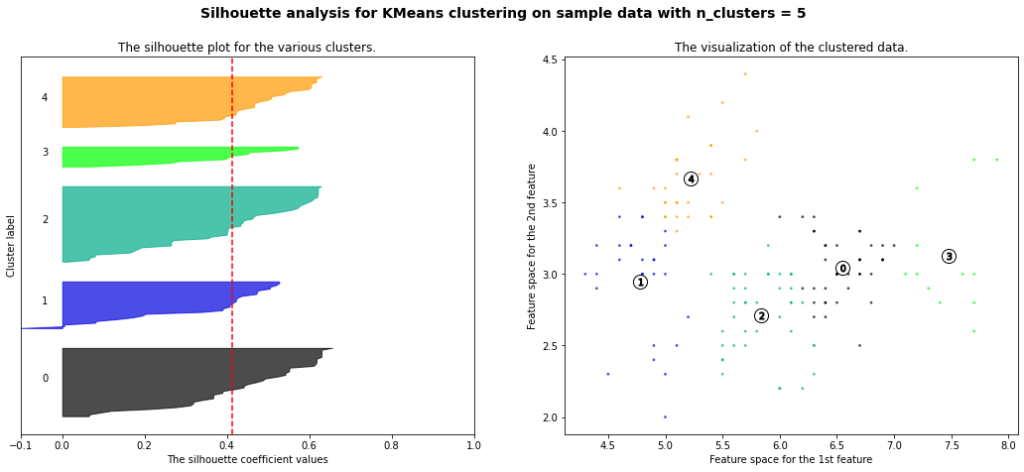
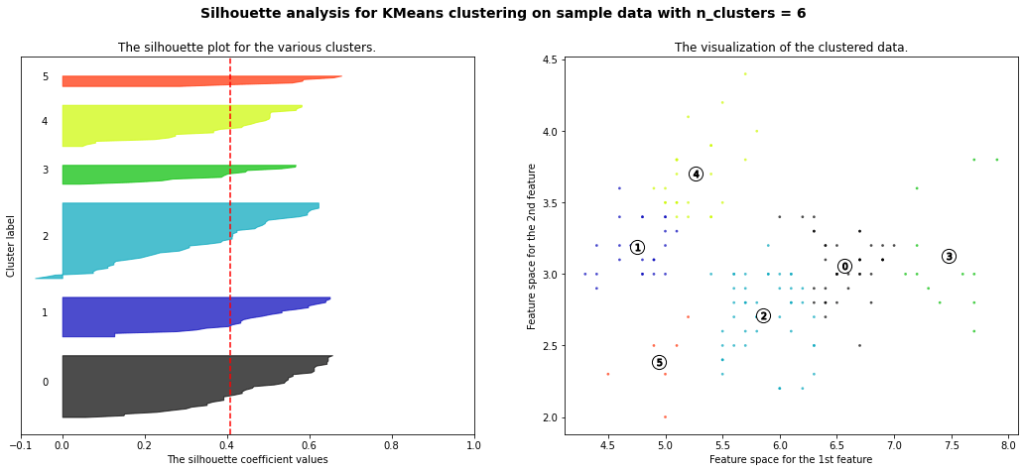
２または３クラスターが比較的良い感じに見えます。というのも、平均シルエット係数が１により近く、全ての帯のデータ数が均等です。また、マイナスに偏ったデータがより少ないものが良ように感じられます。

もともと分け方に正解がないものを分類する難しさと、その評価の難しさがよくわかりました。