自動微分という機能のチュートリアルに入りました。
いきなり自動微分というものが出てきたね。
PyTorchのチュートリアルの2番目に入ったところ、「自動微分(Auto Grad)」という仕組みについて解説がありました。
ニューラルネットワークでは、バックプロパゲーションで勾配降下法などの最適化アルゴリズムのところで微分を利用していることは知っているので、何となくそのあたりの話かなと思っていましたが・・・実際には、「計算グラフ」という微分をより簡潔に計算させるための仕組みを理解していないと、なぜこの自動微分が必要なの?などのいろいろな疑問が生まれてきてチュートリアルどころではなかったのです^^;
今回は、チュートリアルのための前知識ということで、「計算グラフ」が理解できるように頑張ります。
計算グラフについては、がっつりこちらの記事を参考にさせていただきました。
こんな人の役に立つかも
・機械学習プログラミングを勉強している人
・PyTorchのチュートリアルが理解できなかった人
・計算グラフとは何か大まかに知りたい人
計算機での微分
ニューラルネットワークのパラメータを最適化する際に用いられるバックプロパゲーションでは、勾配降下法などを利用して微分をたくさん行います。
数式を愚直にそのまま計算させれば微分ができるらしいのですが、とても遅いらしいです。
そこで、計算速度を上げるためのに「計算グラフ」という方法が利用されます。
計算グラフで考えて微分をするとめちゃくちゃ速度が向上するらしいです。
バックプロパゲーションなどのニューラルネットワークの構成要素については、こちらの記事もご参考ください。

計算グラフ
計算グラフは、計算を構造化して、微分が高速にできるようになる、方法みたいです。
①計算の視覚化(構造化)
計算グラフでは、計算を視覚的に表現(構造的に表現)します。
※プログラムでは、要素同士の繋がりをメモリに記憶したりして表現できるので、構造的、と勝手に表現しています。
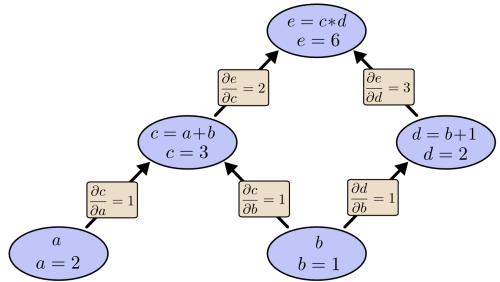
冒頭で紹介しました、参考記事の計算例を引用させていただいて、計算グラフを作成してみます。
(a + b) × (b + 1) = e
前の部分と後ろの部分を次のようにおきます。
・c = a+b
・d = b+1
すると、
・e = c×d
と置き換えることができます。
このように、階層的に計算を行なっていき、一番細かな要素が最終的な答えに結びつくように変換して、次のグラフのように関係を描きます。(参考記事とは違い、横の方がよかったので横にしてみました)
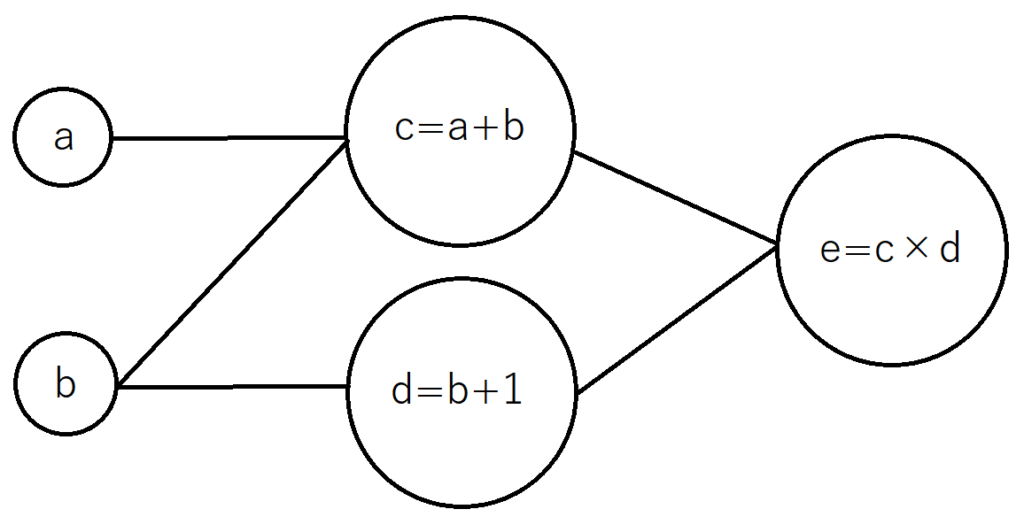
bは、cとdの両方に影響を与えることが一目でわかります。
②計算グラフでの微分
計算グラフの「構造」として計算を把握することで、次のように、要素同士の関係性がわかりやすくなります。
「aの変化量」が「c」に対してどのような影響を及ぼすか?という点に対して、aの変化量に対してcの偏微分を行えば、aの変化量に対するcの変化量、「勾配」が計算できます。
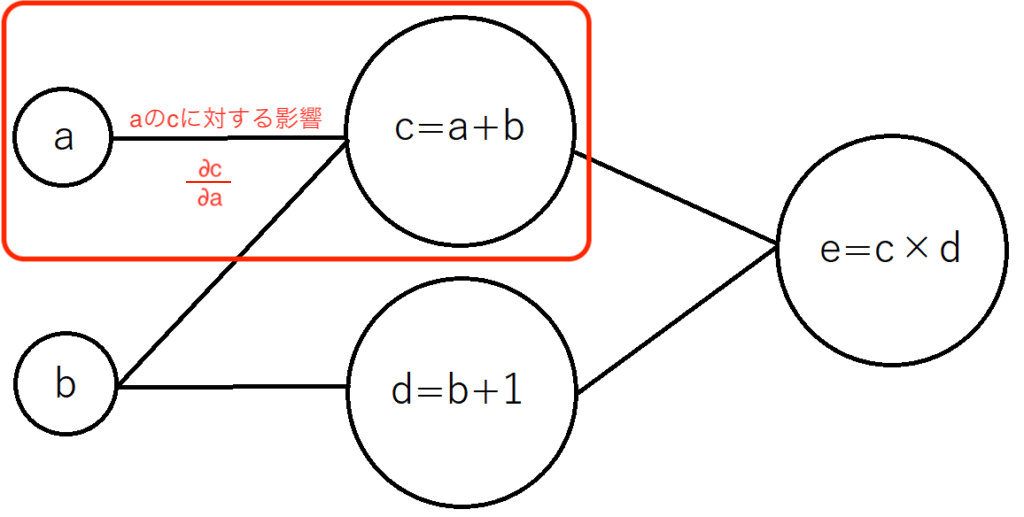
aが「1」変化した時、cは「aの1の変化に対して1変化」(偏微分のためbは固定するという考え方)します。これが、「∂c/∂a」を意味しています。
全ての要素同士の関係性を表現すると、次のようになります。
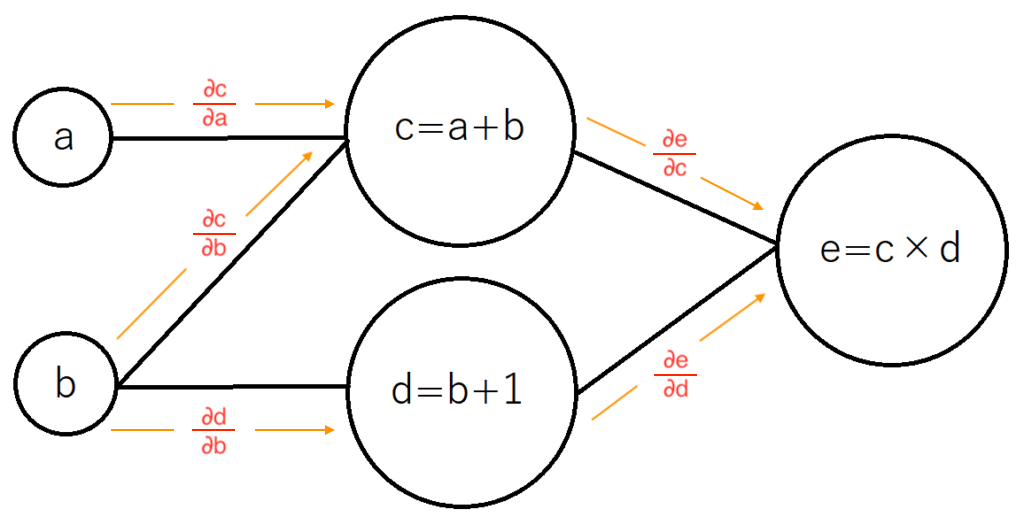
この時、aがeに与える影響はどのように計算できるかというと、次の図のように、①と②を掛け合わせることで、「∂e/∂a」を計算できるのです。
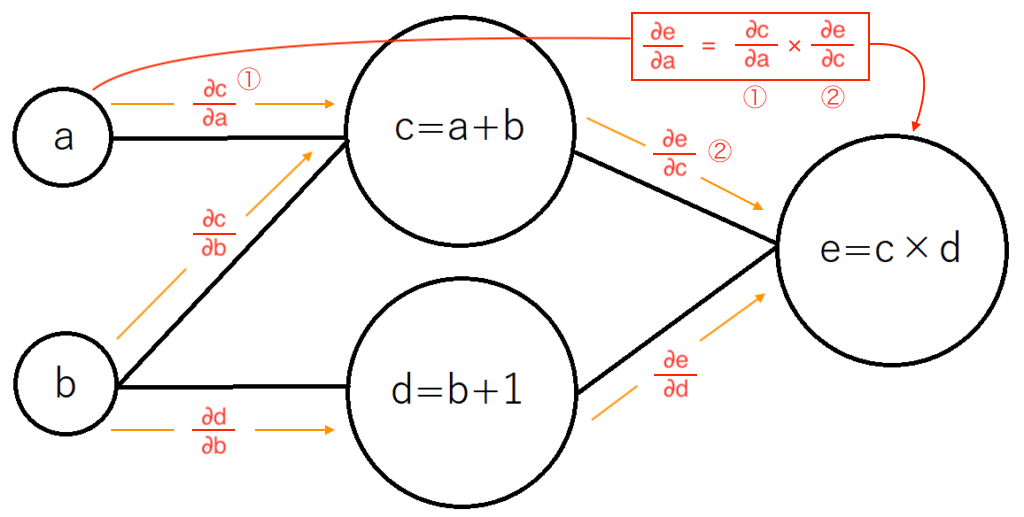
bがeに与える影響である「∂e/∂b」は二つの繋がり方があるので、それぞれの経路を足し合わせる必要があり、計算が「少しだけ」複雑になります。
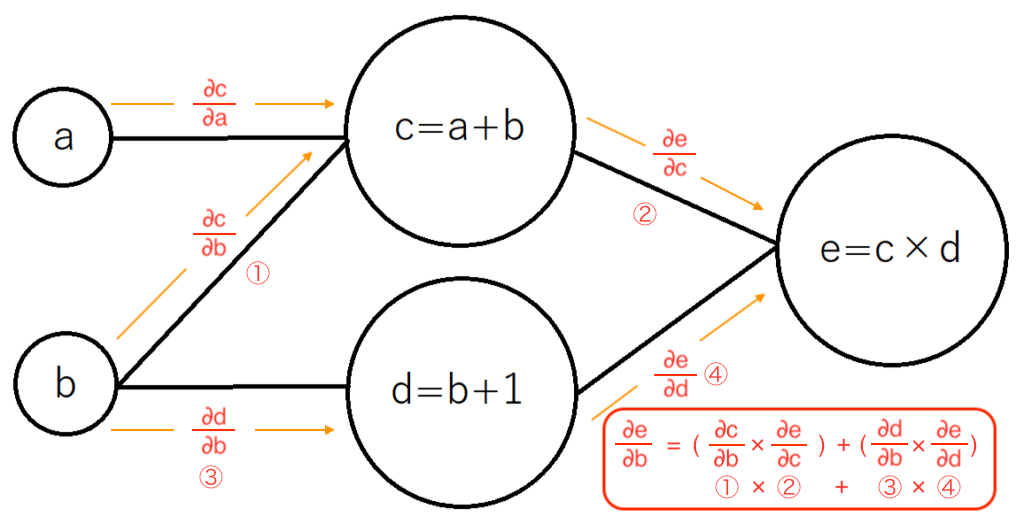
計算が複雑と言っても、「(①×②)+(③×④)」のように、それぞれの微分した値を掛け合わせたり足し合わせたりするだけの計算で微分ができます。これが「自動微分」と呼ばれる所以のように感じます。
計算グラフにすることで、それぞれの要素の微分計算が簡単な式で表現できるようになりました。
まとめると、微分が簡単な計算でパッとできるようになったよ、ということですね。
ちょっとまとめすぎかな〜
計算をする方向
微分を求め始める方向も重要な要素です。
左から(aとbを入力側とします。)微分を行うと、aは赤丸の部分を求めることができます。しかし、bについての微分はまだできていません。そのため、bについての処理も行わなければいけません。
一方、右から微分を行うと、全ての経路へ波及するように計算ができるので、一回の処理ですむという仕組みがあるらしいです。

今回の例はシンプルなので、どちらも同じようなものなのですが、ニューラルネットワークにおいては、「入力が数万、出力は数個」というような関係性が一般的なので、出力側(今回はeの方から)から微分処理を行うと非常に効率がよくなる、ということらしいです。
入力側が数万だと数万回の経路を辿り微分をする処理があり、出力側体と数回で全ての経路がたどることができます。
今回のように、出力側から行う微分処理を、「リバースモード微分」というようで、ニューラルネットワークのバックプロパゲーションには、リバースモード微分が利用されるようです。(入力側からはフォワードモード微分)
確かに、出力側からいけば、全部に繋がるね。
計算グラフまとめ
計算グラフと自動微分について、なんとなく理解できたような(気になっています)感覚なので、大雑把に次のようにまとめたいと思います。
計算グラフは、
⑴計算を構造的、視覚的に表現できる
⑵微分計算を高速に行うことができる
⑶出力と入力の数で処理方向を検討して効率アップ
かなり大雑把・・・
PyTorchのAutoGradについて
ということで、この知識をひっさげて、PyTorchのチュートリアルに戻ってみたいと思います。
PyTorchのAutogradは、この、計算グラフという概念をプログラムに落とし込んだものの・・・はずです。
計算グラフを知らない状態で自動微分のチュートリアルを始めたので、最初何を言っているのか全然わかりませんでした。
どうやらこのチュートリアルは、ある程度ニューラルネットワークのライブラリを触ってきた人が対象のようです。

