ロジスティック回帰をやっていたら、正則化というものが出てきたよ。
正則化をりようしてロジスティック回帰をチューニングできるね。
ロジスティック回帰をいろいろと勉強していました。とても奥が深く、面白いアルゴリズムだなと思います。ロジスティック回帰には、正則化という過学習を防ぐ機能が備わっていて、L1正則化、L2正則化という基本的なものを勉強しました。数学的に理解しようとすると難しそうです^^;
こんな人の役に立つかも
・機械学習プログラミングの勉強をしている人
・ロジスティック回帰の正則化を調整したい人
正則化ってどんなこと?
正則化をすることで、線形モデルの過学習を防ぐことができます。
過学習とは、以前紹介したように、訓練データ特有の個性に合わせてしまい、汎用的でなくなってしまう現象のことでした。
ロジスティック回帰には、正則化という機能がついていて、過学習を防ぐことができるようになっています。
ロジスティック回帰のcのパラメータを大きくすると正則化が弱く、cの値を小さくすると正則化が強くかかるとのことです。
簡単にチューニングできるんですね。
モデルの汎化性能を高めるアルゴリズムのパラメータチューニングの時に、cの値をいい感じに調整してねということだと思っています。
基本的な2種類の正則化
2種類の基本的な正則化のざっくりとした内容も勉強しました。なんとなく理解しておくと、データの形式によってどっちの正則化で行くのかなどの判断材料になるかもしれません。
L1の正則化
L1の正則化は不必要なwを省いてしまう(0にしてしまう)ようにして過学習を防ぎます。wを0にするということは、特徴量を減らしていくことで複雑なモデルから簡単なモデルへとしていきます。
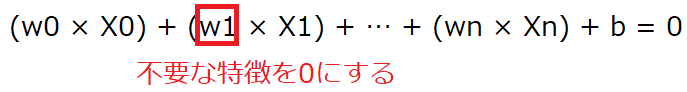
ワイルドな手法です・・・
訓練の過程で、影響のないと判断された特徴量は評価されなくなり、シンプルになるという流れです。
L2の正則化
L2の正則化は、wの数値をできるだけ0に近づけていこうという方向性でモデルの複雑化を防ごうとします。
scikit-learnのロジスティック回帰には、デフォルトでL2という正則化が行われています。
アヤメのデータ分類のプログラム
アヤメのデータ分類でcを調整してみます。
importして、アヤメのデータをロードします。そして、訓練データとテストデータに分割します。ここまでは共通です。
from sklearn.datasets import load_iris
#ホールドアウトのimport
from sklearn.model_selection import train_test_split
#交差検証のimport
from sklearn.model_selection import cross_val_score
#ロジスティック回帰のimport
from sklearn.linear_model import LogisticRegression
import numpy as np
panda_box = load_iris()
X = panda_box.data
y = panda_box.target
#訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, stratify=y)C=0.01
Cを0.01とした正則化の場合です。交差検証を行い、訓練でのスコアを出したのち、訓練を行い、テストデータで評価を行います。
#正則化パラメータC=0.01のロジスティック回帰
cls = LogisticRegression(C=0.01)
#3分割で交差検証を行う。
score = cross_val_score(cls, X_train, y_train, cv=3)
print("交差検証の結果")
print(score)
print("交差検証の平均")
print("{:.4f}".format(np.mean(score)))
#訓練~テスト
cls.fit(X_train,y_train)
print("テストデータの評価")
print("{:.4f}".format(cls.score(X_test, y_test)))訓練の時は、86%でしたが、未知のデータでスコアが出ました。
交差検証の結果
[0.89473684 0.83783784 0.86486486]
交差検証の平均
0.8658
テストデータの評価
0.9211C=0.1
次に、C=0.1としてみました。正則化を弱める方向への変更です。
#正則化パラメータC=0.1のロジスティック回帰
cls = LogisticRegression(C=0.1)
#3分割で交差検証を行う。
score = cross_val_score(cls, X_train, y_train, cv=3)
print("交差検証の結果")
print(score)
print("交差検証の平均")
print("{:.4f}".format(np.mean(score)))
#訓練~テスト
cls.fit(X_train,y_train)
print("テストデータの評価")
print("{:.4f}".format(cls.score(X_test, y_test)))正則化を弱めるとより訓練データに合わせて複雑なモデルとなります。今回は訓練データも正解率が上がり、未知のテストデータにも正解率が上がりました。
交差検証の結果
[0.94736842 0.91891892 0.94594595]
交差検証の平均
0.9374
テストデータの評価
0.9474C=0.5
さらに正則化を弱め、C=0.5で試してみます。
#正則化パラメータC=1のロジスティック回帰
cls = LogisticRegression(C=0.5)
#3分割で交差検証を行う。
score = cross_val_score(cls, X_train, y_train, cv=3)
print("交差検証の結果")
print(score)
print("交差検証の平均")
print("{:.4f}".format(np.mean(score)))
#訓練~テスト
cls.fit(X_train,y_train)
print("テストデータの評価")
print("{:.4f}".format(cls.score(X_test, y_test)))テストデータへの正解率が若干上昇しました。
交差検証の結果
[0.97368421 0.91891892 0.97297297]
交差検証の平均
0.9552
テストデータの評価
0.9474まとめ
今回は、アヤメのデータの特徴量は4つなので、正則化を弱めたほうが(正則化でシンプルなモデルにしないほうが)正解率が良くなる方向がみられました。正則化が有効になってくるのは、もっと特徴量が多いデータに対してもっと有効な感じがしてなりません。
scikit-learnにはガンのデータという特徴量が多いものがあるんだ、それでも試してみたいな。

