何となくライブラリで使ってきましたが、中身について詳しく勉強しないとハイパーパラメータが理解できないと思いました。
なんとなく使えてしまうライブラリってすごいね。
scikit-learnの多層パーセプトロン(MLP)や、keras+tensorflowのニューラルネットワークでチュートリアルを行ってきましたが、ハイパーパラメータの設定は人が行わなければならず、その点は、ある程度ニューラルネットワークの仕組みについて勉強しておく必要がありそうです。プログラミングから離れて、ニューラルネットワーク(ディープラーニングも含む)について勉強を進めています。
keras+tensorflowについては、こちらの記事もご参考ください。

こんな人の役に立つかも
・機械学習プログラミングを勉強している人
・ニューラルネットワークについて大枠を勉強したい人
・ディープラーニングについて知りたい人
ディープラーニングとニューラルネットワーク
ニューラルネットワークの層をたくさん増やしたものがディープラーニングといわれているようです。
実際にアプリなど実用的なものにプログラミングをしようとすると、「畳み込みニューラルネットワーク」のように、具体的なアルゴリズム名を見ることはあっても、ディープラーニングというアルゴリズム名があるわけではありません。
2010年以降になって、
・インターネット、GPU、CPUなどの技術的要素の進歩
・研究の進展
のおかげで、以前は難しかった4層以上のニューラルネットワークの精度が劇的に向上したことが「ディープラーニング」という言葉で総括されているようなイメージでしょうか。
ディープラーニングを勉強するということは、ニューラルネットワークとその発展形を勉強するみたいなイメージなのかな。
ニューラルネットワークの構成要素など
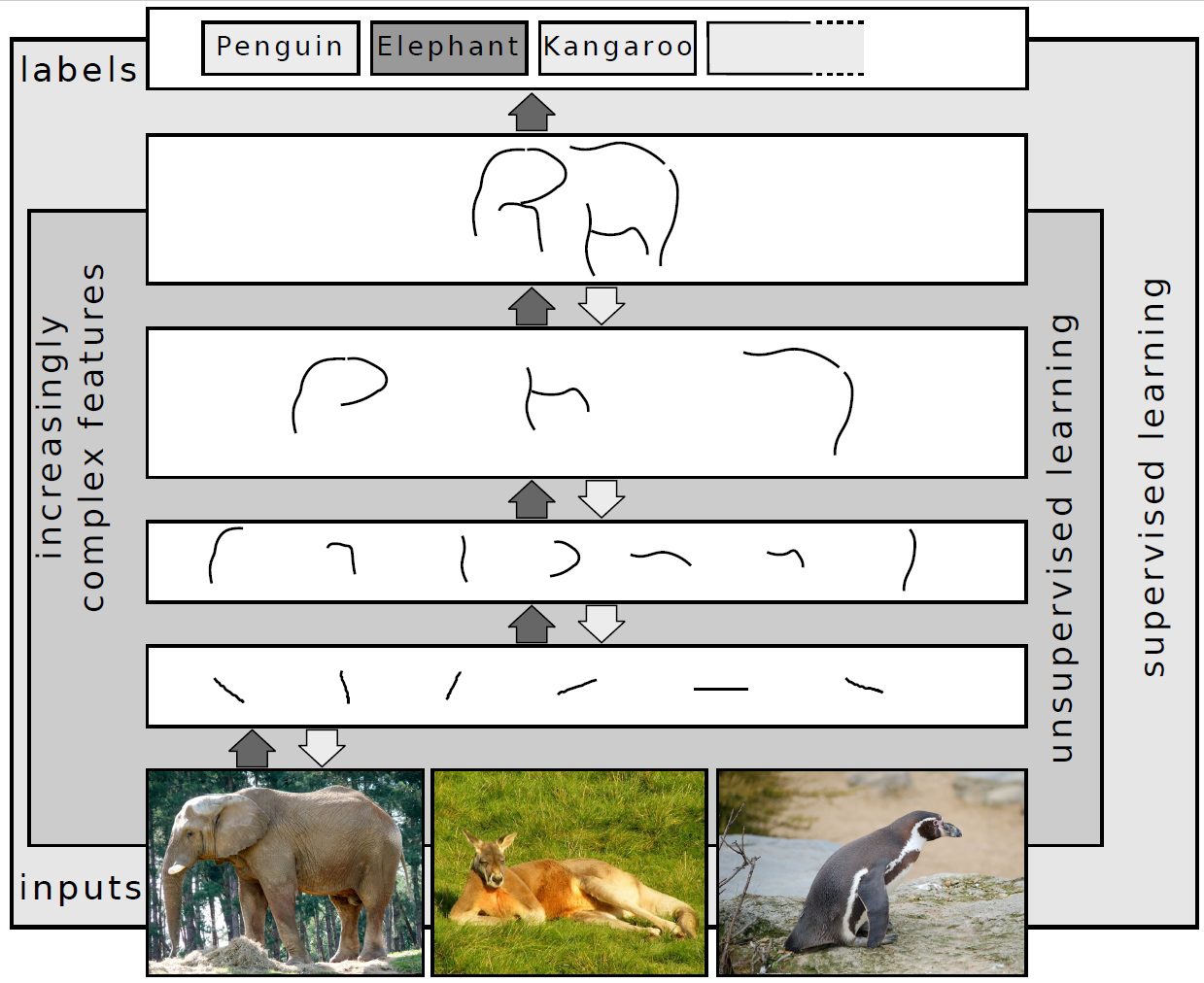
ニューラルネットワークは、主に「教師あり学習」「教師なし学習」を行うことができる機械学習アルゴリズムです。
基本的な形
入力層、中間層、出力層で構成されていて、全結合と呼ばれるものが基本的なニューラルネットワークの形だと思います。
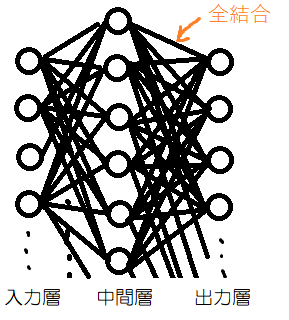
最初にニューラルネットワークを勉強するときは、この形で教師あり学習の分類課題に組むことが多いように感じます。
特に、scikit-learnの「多層パーセプトロン(MLP)」がこの形となっていて、簡単に扱うことができます。

活性化関数
ニューラルネットワークの構成要素の人口ニューロンに活性化関数という概念があります。先ほどのぐちゃぐちゃした全結合ニューラルネットワークは、人工ニューロンを複数寄せ集めてたくさん繋げたものです。
シンプルな人工ニューロンとして、次のように2つの入力と1つの入力がイメージしやすいです。
↓の図は、X1とX2という2つの値を入力に取った場合の人口ニューロンの図です。
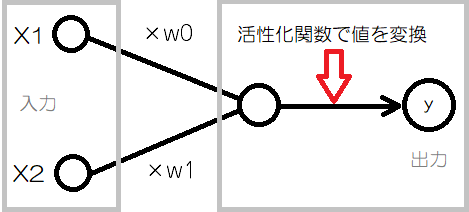
活性化関数がない人工ニューロンは、ただの積の和「(X1×w1)+(X1×w1)」を計算するのみです。
この積の和を「活性化関数」に通して出力を変換することで表現力を与えることができるらしいです。
パーセプトロンは活性化関数がステップ関数の人工ニューロン
活性化関数が「ステップ関数」というものだと、出力「y」を0又は1に変換するので、パーセプトロンのアルゴリズムになります。
一方で、ニューラルネットワークでは、出力の値が連続の値になるような活性化関数が利用されるようです。
よく使われる活性化関数
・ReLU(ランプ関数)
中間層の活性化関数として、「ReLU」が選択されることが多いようです。scikit-learnのMLPもデフォルトでReluが設定されています。
・恒等関数
一般的に、回帰問題の出力層に使われるようです。
・softmax関数
一般的に、分類問題の出力層に使われるようです。
層や、出力する目的によって、活性化関数が使い分けられるようです。
長年の研究で、ある程度よく使われる設定みたいなものがあるんだね。その設定を基準に色々変更してみようと思うよ。
誤差関数
誤差関数は、他にも損失関数、目的関数、コスト関数など、色々な呼ばれ方するらしいです。ややこしい・・・
ニューラルネットワークが出した答えと実際の答えと比較するときに、
「正解とどのように比較するのか?」
というものを定義したものです。
一般的に次のような誤差関数が利用されるようです。
確かに、正解データが9という多クラス問題の答えに対して誤差をどんなふうに定義するかってすごく重要だね。
回帰問題だったら正解との差とかがわかりやすいよね。
一般的な誤差関数
・平均二乗誤差(MeanSquaredError,MSE)
回帰問題では、出力と答えの数値の差を二乗したものを見ることで誤差を見るらしいです。
・交差エントロピー誤差(Cross Entropy error)
分類問題では、交差エントロピー誤差というものを利用して誤差を表現するようです。
誤差関数も、一般的には上のものが利用されることが多いようですが、目的によって変更したりするようです。
誤差関数がどこで利用されるのか?
誤差関数は次のように訓練で利用されます。
教師あり学習で「訓練」を行う際には、
①「まとまったデータを与える」
②「誤差の方法で誤差を算出」
③誤差を小さくする方向にニューラルネットワークの重みを調整
というようにしてより良いパラメータ(ニューラルネットワークの重みのw0やw1など0)を探索していきます。
そして、より良いパラメータを探索する上の①〜③の手順は、勾配降下法と呼ばれる方法で実現されます。
ニューラルネットワークには、すごく色々な要素があります。
まだまだ勉強の余地がありますな。
今回は、ニューラルネットワークが備えている「活性化関数」や、「誤差関数」と行った仕組みについてどんなものがあるのかを学びました。
次は、訓練に関わるバックプロパゲーションや勾配降下法などの要素についてもみていきたいと思います。
次の記事はこちらです。