リッジ回帰とは違った過学習を防ぐ手段を備えたLasso回帰を勉強したよ
RidgeとLassoはセットで覚えるみたいだね
Ridge回帰は線形回帰の重みを0に近づける方向に補正をかけることで、回帰モデルの複雑化を抑制するというものでした。これは、L2ノルムという項を二乗誤差に追加することで重みが必要以上に大きくなりすぎてしまうという現象を防ぐものでした。もう一つのL1ノルムというもので過学習を防ぐような効果のあるLasso回帰というものがあります。今回はLasso回帰を利用してボストン住宅モデルの回帰を行いました。
こんな人の役に立つかも
・機械学習プログラミングを勉強している人
・Lasso回帰について勉強している人
・scikit-learnのLasso回帰の勉強をしている人
Lasso回帰
まずはLasso回帰について
Lasso回帰は、L1ノルムという正則化をおこなってモデルが訓練データに適合しすぎることを防ぐものです。
Lassoは「Least absolute shrinkage and selection operator」の略で、この名前からも、特徴量を選択する、という意味が伝わってきます。
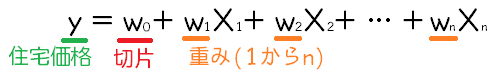
Ridge回帰は、L2ノルムというもので、w1~wnまでの重みを0に近づけるよう(出来るだけ小さい値に)に抑えるようにしていました。
それに対して、Lasso回帰ではL1ノルムというものを使い、影響が少なそうな特徴量の重みwを完全に0にしてしまいます。これは、特徴量を選択している効果と同じになります。
以前、分類問題の正則化でも勉強したL1ノルムと同じ効果があるんだね。
以前、ロジスティック回帰の分類問題を勉強していた時も、正則化について勉強をしました。L1ノルム、L2ノルムという数学的な項を追加することで、wの重みを抑制することができる数学的操作です。正則化についてはこちらの記事もご参考ください。

普通にLossoを使って予測するプログラム
Ridge回帰の時と同様に、LinearModelなどをimportします。そして、特徴量は、多重共線性を避けるように選択しました。
多重共線性については、こちらの記事もご参考ください。

from sklearn.datasets import load_boston
from sklearn import linear_model
from sklearn.model_selection import train_test_split
panda_box = load_boston()
X = panda_box.data
y = panda_box.target
#0:CRIM 1:ZN 2:INDUS 3:CHAS 4:NOX 5:RM 6:AGE 7:DIS 8:RAD 9:TAX 10:PTRATIO 11:B 12:LSTAT
X = X[:,[0, 1, 2, 3, 5, 8, 10, 11, 12]]
#訓練データとテストデータに分割(テストデータ25%)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25)そして、linear_modelからalpha=1としてLasso回帰を呼び出してそのままX_trainとy_trainのデータで学習させます。学習させたモデルが変数「Lasso」に入ります。
最後にテストデータを入れて予測精度を評価します。もちろん、今まで通り、予測精度は決定係数になります。
最後に、「coef_」を表示することで、Lasso回帰で求められたボストン住宅価格データに対する重回帰のすべての重みを表示することができます。
#Lasso回帰モデルを訓練して作成
Lasso = linear_model.Lasso(alpha = 1, max_iter=100000).fit(X_train,y_train)
#テストデータに対する精度を評価
print(Lasso.score(X_test,y_test))
#Lasso回帰で得られた重みを表示
print(Lasso.coef_)0.6799846733092159
[-0.02249818 -0. -0. 0. 1.26370273 0.07964015
-0.9182561 0.0112785 -0.74304607]興味深いのが、2番目、3番目、4番目の特徴量の重みが0となっています。重みを0にするということは、0×特徴量になるので、その特徴量の影響が全くなくなることになります。
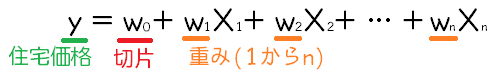
改めて、ワイルドな手法・・・
リッジ回帰と比較
ちなみに、同じデータでRidge回帰を行うと、精度と重みはこうなりました。alphaのパラメータはLasso回帰と同じ1にしてみました。パラメータは方向性が違うので、同等の効果とは言えませんが、とりあえず1という同じ数値にしてみました。
#同じデータでリッジ回帰
Ridge = linear_model.Ridge(alpha=1).fit(X_train,y_train)
print(Ridge.score(X_test,y_test))
print(Ridge.coef_)リッジ回帰のほうが若干精度が高く、また、正則化の方向性も大きくなりすぎる重みを押さえるという感じになっています。
0.7272623255381445
[-0.03488979 -0.00859263 -0.01284573 3.60449183 4.27797353 0.10259673
-0.9630466 0.0138135 -0.57355111]リッジ回帰のほうが大人な感じがするね。
みんな(特徴量)の意見を大事にしているところが大人だね。

