もう少しプログラムを複雑にしてアニメーションも複雑にしていきます。
GUI表現の一つとして、勉強になるね~
JUCEチュートリアル、「Graphics」の「Animating geometry」チュートリアルの続きです。今回は、「Animating a Path」の項目からになります。
公式のチュートリアルページはこちらになります。
https://docs.juce.com/master/tutorial_animation.html
こんな人の役に立つかも
・JUCEプログラミングを勉強している人
・JUCEチュートリアル「Animating geometry」をやっている人
・JUCEアプリにアニメーションを導入したい人
アニメーション処理を複雑に
paint関数内の処理を書き換えることで、少し複雑なアニメーションをウィンドウに表示していきます。
paint関数の中を次のように変更しました。
void MainComponent::paint(juce::Graphics& g)
{
g.fillAll(getLookAndFeel().findColour(juce::ResizableWindow::backgroundColourId));
g.setColour(getLookAndFeel().findColour(juce::Slider::thumbColourId));
auto numberOfDots = 15;//[1]パスに追加する点の数です。
juce::Path spinePath;//[2]juce::Pathオブジェクトの定義です。
//[3]Pathの描画設定です。
for (auto i = 0; i < numberOfDots; ++i)
{
int radius = 150;
juce::Point<float> p((float)getWidth() / 2.0f + 1.0f * (float)radius * std::sin((float)getFrameCounter() * 0.04f + (float)i * 0.12f),
(float)getHeight() / 2.0f + 1.0f * (float)radius * std::cos((float)getFrameCounter() * 0.04f + (float)i * 0.12f));
if (i == 0)
spinePath.startNewSubPath(p);//[3-1]パスの最初の点です。
else
spinePath.lineTo(p);//[3-2]2つ目以降のPathの点です。
}
//[4]Pathオブジェクトを描画します。
g.strokePath(spinePath, juce::PathStrokeType(4.0f));
}Paint関数で変更した点としては、juce::Pathを利用して描画を行うようにした点です。
[1]では、Pathに追加する点の数を定義して、[2]で描画対象のPathオブジェクトの定義、[3]でPathの描画設定を行います。[4]で、Pathを描画しています。
[3]のループでは、iが変化するたびに最後の係数「i*0.12f」が変化していきますので、1度のpaint関数の[3]のループで15点のパスが作成されます。次のようなイメージで15点打つことになります。
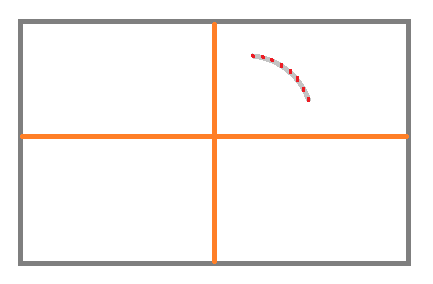
[3-1]の「startNewSubPath」関数は、パスの開始点となるときの関数です。iが0のときという条件で分けています。[3-2]からの「lineTo」関数で、2つの座標を結ぶラインを作成します。
https://docs.juce.com/master/classPath.html
また、次のPaint関数が実行されると、getFrameCounterの値も変化するので、SinやCosの係数が前回のPaint関数から変化しています。Sinを例に、横の揺れのイメージは次のようになるでしょうか。
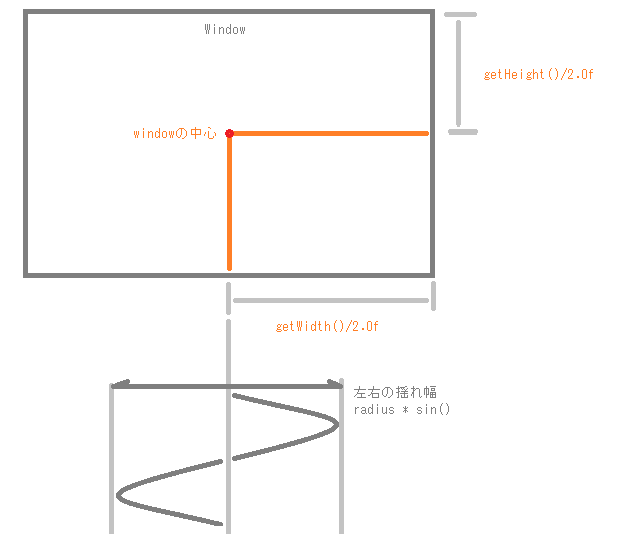
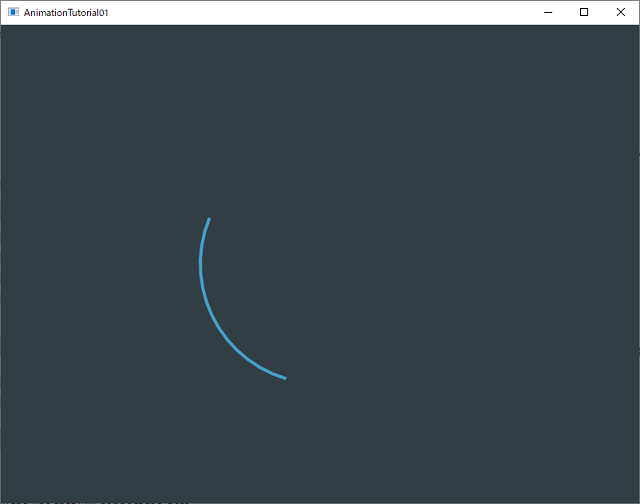
これらが複合的にくりかえされて、円弧が回転するようなアニメになりました。
Animating a Fish
チュートリアルでは先ほどの円弧に円を追加して、円弧の動きをうねうねさせるようにして魚が泳いでいるようなアニメーションを作ります。何段階かに分けて最終的にランダムに動いているように見えるような魚のようなアニメーションを作成しますが、ここでは、一度に変更して、変更点を見てみます。
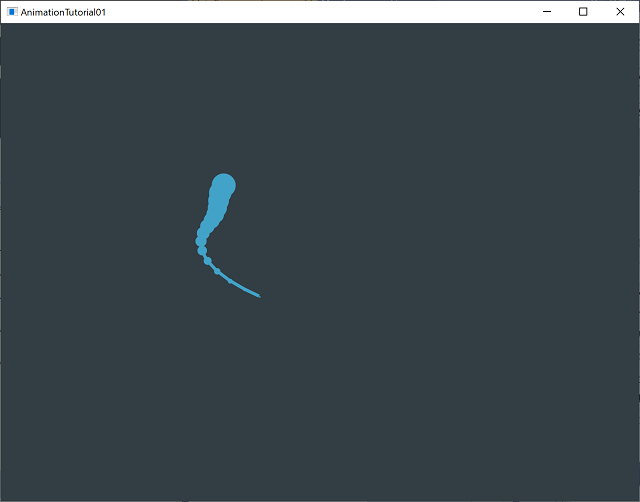
ウネウネ♪
次のようにPaint関数を変更しました。
void MainComponent::paint(juce::Graphics& g)
{
//...略...
for (auto i = 0; i < fishLength; ++i)
{
//[1]radiusを変動させるように変更しました。
auto radius = 100 + 10 * std::sin(getFrameCounter() * 0.1f + i * 0.5f);
//[2]座標Xのsinに与える係数などの変更です。
juce::Point<float> p(getWidth() / 2.0f + 1.5f * radius * std::sin(getFrameCounter() * 0.02f + i * 0.12f),
getHeight() / 2.0f + 1.0f * radius * std::cos(getFrameCounter() * 0.04f + i * 0.12f));
//[3]円を描く関数です。
g.fillEllipse(p.x - i, p.y - i, 2.0f + 2.0f * i, 2.0f + 2.0f * i);
//...略...[1]では、radiusを変動するようにしています。sin関数のラジアンとして、getFrameCounterに0.1をかけた値とループ変数iに0.5をかけた値を与えてsinの変動スピードを決定します。sinは-1~1の間で変動しますので、radias変数は90~110の間で変動します。これは、今まで150固定だった円の半径が常に大きくなったり小さくなったりする動作となります。
[2]では、PointクラスpのX座標のradiusに掛け合わせる係数1.5fとSinに与える係数0.02fをY軸方向の動作のcosと違いを与えることで、X軸とY軸の位相がずれる(という表現でよいかわかりませんが)ようなイメージで動作に揺らぎが出てきます。
[3]は、pの点に円を描く関数「fillEllipse」で魚の本体を表現しています。
これを1回のpaintで15回繰り返すことで魚の形を形成します。
テー〇の洞穴のボスのようですね。

