【AIプログラミング】決定木で分類を行う、境界線の可視化

決定木というものを勉強しました。決定木は機械学習の手法でも、比較的イメージしやすいらしく、また、最近の機械学習のコンペでもいい性能を出している手法のベースとなっているようで、是非とも勉強しておきたいものです。まずは、決定木で乳がんデータの特徴量２つを利用して、分類をおこない、どんな境界線ができるかを確認してみました。

こんな人の役に立つかも

・機械学習プログラミングの勉強をしている人

・決定木について勉強している人

・scikit-learnで決定木の境界線を引きたい人

決定木についてざっくりと知る

決定木は、教師あり学習で、「分類」にも「回帰」にも利用できます。分類に利用した時、次の図のようなイメージです。

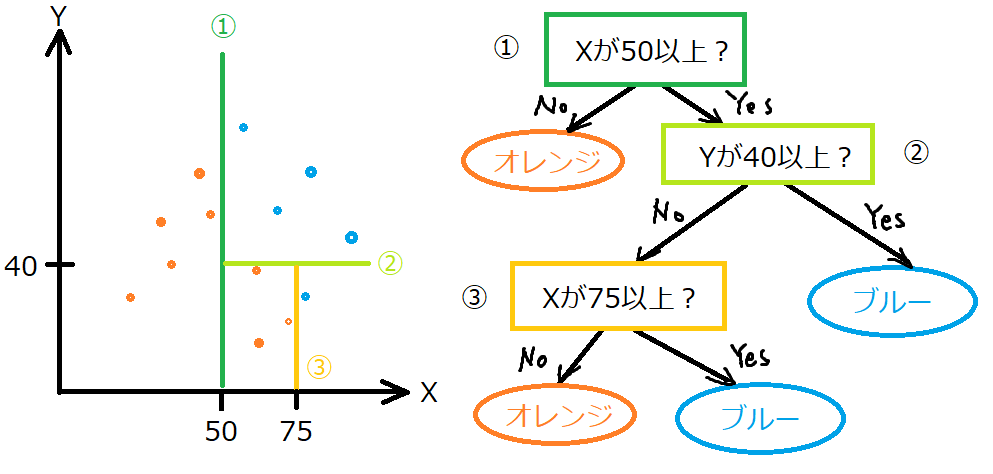
決定木は、訓練データを訓練させることで、図のような境界線を作成します。左図の境界線は１つ１つが右図のような条件になっています。

例として、①はXが50以上の時、はい、いいえによって答えに行き着くか、次の条件にいくか・・・といった感じです。そして、今回のイメージでは、③までの深さなので、「深さが３の決定木」となります。

プログラムで、分類に利用した時に、どのような境界線になるのかなどをみていきます。

プログラムで境界線の確認

決定木のプログラミングの準備

importからscikit-learnの乳がんデータを読み込みます。

乳がんデータについてよくわからないという方は、乳がんデータについてのこちらの記事もご参考ください。

今回は、二次元のグラフとして可視化したいので、「X = panda_box.data[:,0:2]」で30個ある乳がんデータの特徴量を２個に絞っています。

特徴量として、１番目と２番目の特徴量「mean radius」「mean texture」を選択しました。

from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn import tree
import matplotlib.pyplot as plt
import numpy as np

#乳がんデータ
panda_box = load_breast_cancer()

#2個分の特徴量に絞る
X = panda_box.data[:,0:2]
y = panda_box.target

次に、データを訓練データとテストデータに分割します。

その後、データを標準化しています。標準化は、データのスケール感を合わせるような処理です。

標準化については、こちらの記事もご参考ください。

#訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, stratify=y, random_state=0)

#標準化
from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
#訓練データをもとに標準化して訓練データを標準化
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

データのスケールに依存しない決定木

標準化したデータを決定木にかけて、分類してみます。交差検証で行います。標準化したデータは「X_train_scaled」に入っています。

交差検証に関しては、こちらの記事もご参考ください。

#標準化したデータに対する評価
#決定木
clf = tree.DecisionTreeClassifier()

#交差検証
score = cross_val_score(clf, X_train_scaled, y_train, cv=3)

#結果の表示
print("標準化データに対する評価")
print("交差検証の結果")
print(score)
print("交差検証の平均")
print("{:.4f}".format(np.mean(score)))

"標準化データに対する評価"
"交差検証の結果"
[0.88028169 0.85211268 0.82394366]
"交差検証の平均"
0.8521

次に、標準化していないデータで訓練してみます。

#標準化していないデータに対する評価
clf2 = tree.DecisionTreeClassifier()
score2 = cross_val_score(clf2, X_train, y_train, cv=3)

#結果の表示
print("標準化していないデータに対する評価")
print("交差検証の結果")
print(score)
print("交差検証の平均")
print("{:.4f}".format(np.mean(score)))

"標準化していないデータに対する評価"
"交差検証の結果"
[0.88028169 0.85211268 0.82394366]
"交差検証の平均"
0.8521

決定木の境界線を可視化しよう

以前、記事にした、境界線を引く機能を利用します。こちらもご参考ください。

次のような「関数」を二つ用意して、次のプログラムで利用します。

#関数を作成
def make_meshgrid(x, y, h=.02):
    x_min, x_max = x.min() - 1, x.max() + 1
    y_min, y_max = y.min() - 1, y.max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                         np.arange(y_min, y_max, h))
    return xx, yy

def plot_contours(ax, clf, xx, yy, **params):
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    out = ax.contourf(xx, yy, Z, **params)
    return out

次に、決定木を「深さ３」で準備します。そのまま、標準化されたデータで訓練をしています。

#決定木
clf = tree.DecisionTreeClassifier(max_depth=3).fit(X_train_scaled[:,0:2],y_train)

#空のグラフを作成
fig = plt.figure(figsize=(9, 4))
ax = fig.add_subplot(121)

#グリッドのデータを作成
X0 , X1 = X_train_scaled[:,0], X_train_scaled[:,1]
xx, yy = make_meshgrid(X0, X1)

#グラフに境界線とデータをプロット
plot_contours(ax, clf, xx, yy, cmap=plt.cm.coolwarm, alpha=0.8)
ax.scatter(X0, X1, c=y_train, cmap=plt.cm.coolwarm, s=20, edgecolors='k')

境界線を引くとこのようになりました。

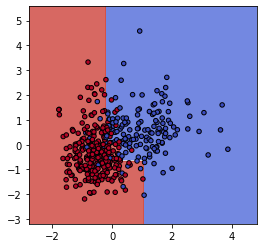
決定木の「max_depth=3」をもっと大きな値にしてみます。深さ５にしてみました。

決定木は、制限をしないと訓練データを過学習しやすいので、深さを制限するなどの処置が必要です。

まとめ：今回勉強した決定木

今回決定木を勉強した内容としては、次のような項目が重要でした。

・回帰問題、分類問題の両方に利用できる。

・標準化は効果がない。

・過学習しやすいのでチューニングが重要。

まだ決定木について十分に知れていないので、もう少し決定木について深めていきたいです。