今までは、何気なく利用してきたk最近傍法の境界線がどうなっているか?
境界線を視覚化したいと思います。
前回は、機械学習アルゴリズムを理解するために、アヤメのデータを2次元化しました。とりあえずk最近傍法がどんなふうに分類してくれるかの境界線を描画してみました。
アヤメのデータを2次元に限定する方法については、こちらの記事もご参考ください。

こんな人の役に立つかも
・機械学習プログラミングを勉強している人
・scikit-learnでk最近傍法のプログラミングを勉強している人
・教師あり学習、分類の境界線を可視化したい人
境界線を可視化しよう
k最近傍法でアヤメデータを分類し、その境界線を可視化していきます。
importから、アヤメデータを2次元化
まずは、importから、アヤメのデータを2次元、2クラスのデータにします。グラフで可視化できるように、シンプルなデータにします。
#k-最近傍法のimport
from sklearn.neighbors import KNeighborsClassifier
import numpy as np
import matplotlib.pyplot as plt
panda_box = load_iris()
X = panda_box.data
y = panda_box.target
#2次元のアヤメデータを作成
X_2dim = panda_box.data[:,:2]
#アヤメデータを2クラス(「setosa」と「versinica」のみ)に絞り込む
X_2dim_2cls = X_2dim[y!=2]
y_2cls = y[y!=2]2次元化する理由としては、イメージしやすいためです。
境界線を可視化するプログラム
次に、境界線を可視化するためのプログラムをいくつか作成しておきます。
defというキーワードで、関数という繰り返し使えるプログラムの部品を作成します。
今回は、scikit-learnの「Plot different SVM classifiers in the iris dataset」というドキュメントを参考に、視覚化するプログラムを作成しました。

#3つの関数を作成
def make_meshgrid(x, y, h=.02):
x_min, x_max = x.min() - 1, x.max() + 1
y_min, y_max = y.min() - 1, y.max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
return xx, yy
def plot_contours(ax, clf, xx, yy, **params):
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx, yy, Z, **params)
return out
#ここはオリジナルの関数です。
def graf_setting(ax):
ax.set_xticks(())
ax.set_yticks(())
ax.set_xlabel('Sepal length')
ax.set_ylabel('Sepal width')「make_meshgrid」という関数と「plot_contours」という関数は、先ほどのscikit-learnのドキュメントと同じものです。
「graf_setting」という関数は、グラフの装飾を行うものをまとめました。
とりあえず、上記3つの関数を作成しておいて、利用することでグラフに機械学習アルゴリズムの境界線を描くことができます。
「make_meshgrid」と「plot_contours」の細かい内容については、おいおい理解していきたいと思います。
k最近傍法で分類して境界線を可視化
#k最近傍法の作成
model = KNeighborsClassifier(n_neighbors = 1)
#k最近傍法の訓練
clf = model.fit(X_2dim_2cls, y_2cls)
#空のグラフを作成
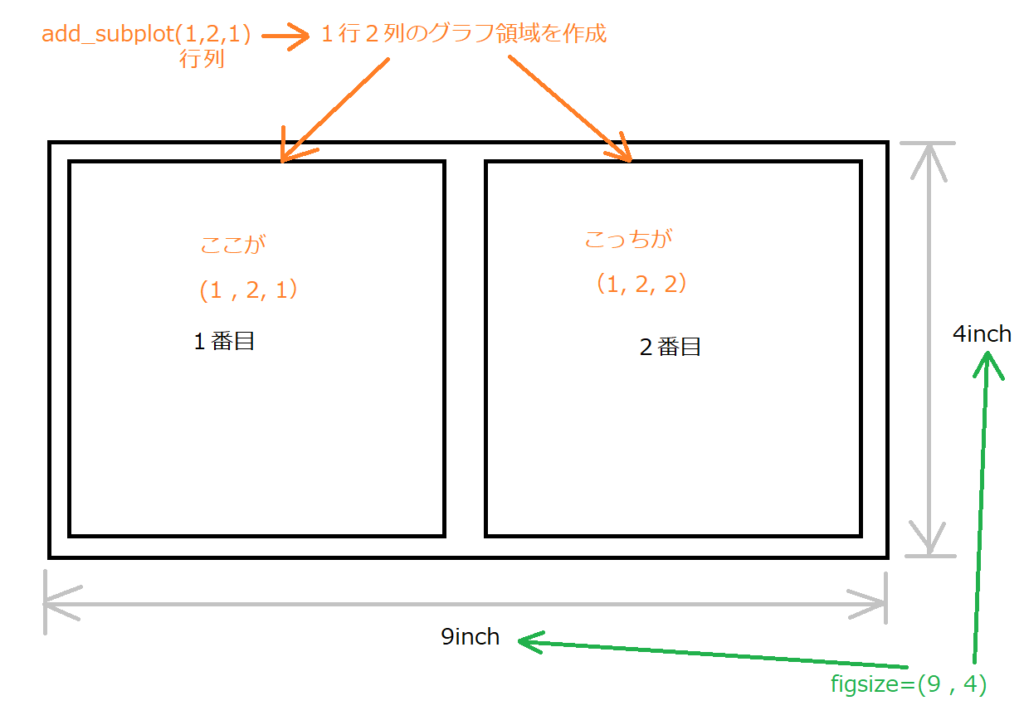
fig = plt.figure(figsize=(9, 4))
ax = fig.add_subplot(121)
#グリッドのデータを作成
X0, X1 = X_2dim_2cls[:, 0], X_2dim_2cls[:, 1]
xx, yy = make_meshgrid(X0, X1)
#グラフに境界線とデータをプロット
plot_contours(ax, clf, xx, yy, cmap=plt.cm.coolwarm, alpha=0.8)
ax.scatter(X0, X1, c=y_2cls, cmap=plt.cm.coolwarm, s=20, edgecolors='k')
graf_setting(ax)k最近傍法を作成して、訓練します。今回は、訓練後の境界線をひくだけなので、テストデータと訓練データに分けてはいません。
その後、#空のグラフの作成部分にて、グラフを描く下準備をします。
最後に、先ほど作成した3つの関数「make_meshgrid」と「plot_contours」、「graf_setting」を使用して、k最近傍法の境界線の色付けを行いました。
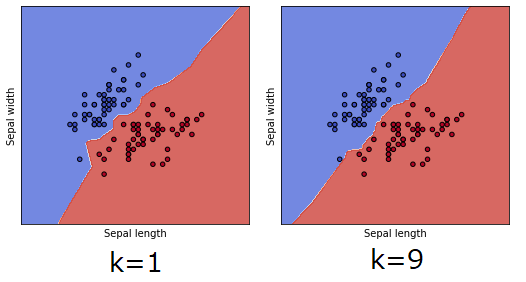
イメージ通り、kの値を大きくしていくと、境界線がなめらかに直線に近くなっていくね。
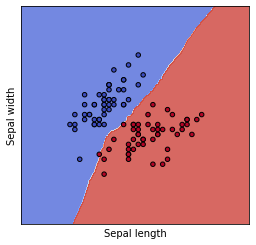
k=32となると、かなり境界線の形が変形して生きています。
k最近傍法でkの数を調整することはかなり大事ですね。
可視化プログラムの詳細
こちらの記事で、境界線を可視化するプログラムをさらに詳しく紐解きます



