scikit-learnのボストン住宅価格のデータ観測、データをプロット

アヤメのデータの時にもmatplotlibというグラフの視覚化ライブラリでデータのばらつきを視覚化しました。今回も、ボストンの住宅価格のデータをプロットしていきます。

前回の記事もご参考にどうぞ。

こんな人の役に立つかも

・機械学習プログラミングの勉強をしている人

・ボストン住宅価格データについて知りたい人

・matplotlibで散布図を作成したい人

プログラムでボストン住宅価格データ散布図

１３ある特徴量と住宅価格「MEDV」のデータにはどのような関係性がありそうか、それぞれの特徴量と「MEDV」との散布図を作成して、目視で確認をしてみます。

こんなグラフを作成してみます。

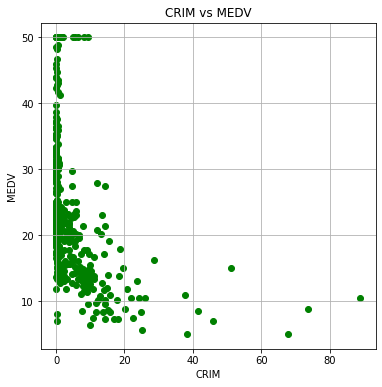
例えば、住宅が存在している地域の１人当たり犯罪率を横軸に、住宅価格を縦軸に取ったときの散布図です。

この散布図から、犯罪率が低い地域には、低価格の住宅から高価格の住宅までまんべんなく存在していますが、犯罪率が高い地域には比較的安い住宅のみが存在していることがわかりました。

散布図にすることで、データの傾向や、おかしなデータが含まれていないか、などが目視で確認できます。

importからデータの前処理

scikit-learnからボストンの住宅価格データの読み込みを行います。

pandasも少し使うので、importしています。

#scikit-learnからボストン住宅価格データのimport
from sklearn.datasets import load_boston
#データを表形式にするためのpandasをimport
import pandas as pd

panda_box = load_boston()

print(panda_box.feature_names)

特徴量をprintしておくと後から便利だと思ったので、feature_namesをprintして表示しています。

['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
 'B' 'LSTAT']

欠損値の確認

まず最初に、pandasのデータフレームという形に変換して、データに欠値がないかという確認を行います。

※今回はscikit-learnの使い古された定番データなので、欠損値はないのですが、自分で集めたデータには、データの入力ミスなどで生じた、イレギュラーなデータを事前に確認することが大事とのことなので、やってみます。

pandasのDataFrameという形に変換すると、isnull()という機能が使用できます。isnullはデータがないものを探すことができる機能で、一部データが欠けているものがないかどうかを探すことができます。

#ボストン住宅価格データ
#１３の特徴量が存在
data_df = pd.DataFrame(panda_box.data)
#欠損データの確認
print(data_df.isnull().sum())
#住宅価格データ
target_df = pd.DataFrame(panda_box.target)
#欠損データの確認
print(target_df.isnull().sum())

pd.DataFrame(panda_box.data)とすることでボストンの住宅データをpandasのデータフレームという形に変換しています。それをdata_df(命名自由)という変数に入れています。

その後、data_df.isnull()とすることでデータに欠損値がないかを調べることができます。isnullだけで表示するとすべてのデータに対して（506個の結果）が出てしまうので、その中で欠損があったデータの個数だけを数えるため、sum()という機能でカウントしています。このようにすることで、特徴量別に、欠損値のあるデータが何個存在するかを表示することができます。

同様に、targetのデータ（MEDVのデータ）に対してもisnullでチェックを行いました。

欠損しているデータがないことが確認できました。

散布図を描く

次のプログラムで、「13個の特徴量」vs「住宅価格(MEDV)」をすることができます。

select_xという変数に、コメントアウトしてある特徴量の番号を参考に数値を入力しておくと、select_xに指定した特徴量vs「MEDV」の散布図を描きます。

import matplotlib.pyplot as plt
#0:CRIM 1:ZN 2:INDUS 3:CHAS 4:NOX 5:RM 6:AGE 7:DIS 8:RAD 9:TAX 10:PTRATIO 11:B 12:LSTAT
select_x = 12
_df = panda_box.data[:,select_x]

plt.figure(figsize=[6,6])
plt.scatter(_df,target_df, c="green")
plt.title(panda_box.feature_names[select_x] + ' vs MEDV')
plt.xlabel(panda_box.feature_names[select_x])
plt.ylabel('MEDV')
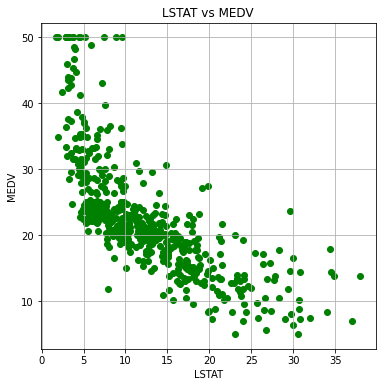
plt.grid(True)

上の例では、select_xに12（LSTAT）を指定したので、低階級の人の多さと住宅価格の関係を散布図に表現しています。

散布図からデータを観測

グラフでいろいろ確認したところ、先ほどの１２の「LSTAT」と、６の「RM」がきれいに住宅価格と関連していそうな散布図になりました。

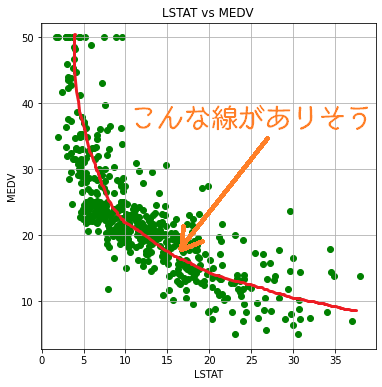
「低階級の人の多さ」(LSTAT)が大きいと住宅価格は低くなる傾向にある。

「部屋数」が多くなるほど住宅価格が高くなる傾向がある。

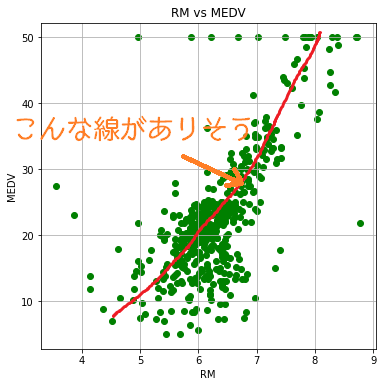
こんな関係性がありそうです。

今回、「１つの特徴量」VS「住宅価格」という関係性を見ています。一つの特徴量（一つの説明変数）で目的変数（住宅価格）が決定されるようなモデルが上で描いた赤線になりますので、「単回帰」を行っていることになります。

まずは、住宅価格と関係性がありそうな特徴量について、単回帰をするプログラムに挑戦してみたいと思います。