【Aiプログラミング】リッジ回帰でボストン住宅価格データの回帰をする

今回、リッジ回帰というものを勉強しました。正直、何となく数学的な計算イメージはわかるのですが、いろいろ調べると統計学の深いお話が出てきたりして、だんだん頭が痛くなってきました　笑

とりあえずリッジ回帰をscikit-learnのボストン住宅価格データで試して、上澄みの知識をアップデートしましたので、その備忘録まで。

こんな人の役に立つかも

・機械学習プログラミングを勉強している人

・リッジ回帰についてふわっと知りたい人

リッジ回帰は何がいいの？

線形回帰では、下のような式で、目的変数（y）を予測する前提で、実データからちょうど良いw0～wnを導き出すという感じでした。ただ、特定のw(重み)が大きくなりすぎると、特定の特徴量にフィットしすぎてしまい、訓練用データのみに有効な予測式になってしまいます。これを「過学習」といいました。

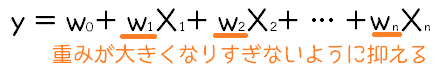
そこで、「L2正則化項」というものを足すことでw（重み）が大きくなりすぎないようにして、過学習を防ごう！というものです。

最小二乗法の時は、二乗誤差を最小にするように重みと切片を計算しましたが、この二乗誤差にL2正則化項を足したものを最小化するようにします。これはscikit-learnのリッジ回帰をfitさせるときにやってくれますので安心ですね。

scikit-learnでリッジ回帰のプログラミング

リッジ回帰は、線形回帰と同様、scikit-learnの「linear_model」にふくまれていますので、今までとおなじimportで利用することができます。

#リッジ回帰
from sklearn.datasets import load_boston
from sklearn import linear_model
from sklearn.model_selection import train_test_split

panda_box = load_boston()

X = panda_box.data
y = panda_box.target

#訓練データとテストデータに分割(テストデータ25%)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25)

リッジ回帰のパラメータ「alpha」を調整することでチューニングを行うことができます。パラメータ「alpha」が0で、何も調整されない状態で、数値を大きくすることで係数を小さく抑えることができます。

今回は、0、0.1、0.5、1という４つのパターンでリッジ回帰をおこなってみました。

#Ridge回帰を作成して訓練させる
reg = linear_model.Ridge(alpha=0).fit(X_train,y_train)

print("alpha=0")
print("訓練データへの決定係数　：{:.3f}" .format(reg.score(X_train, y_train)))
print("テストデータへの決定係数：{:.3f}" .format(reg.score(X_test, y_test)))

reg = linear_model.Ridge(alpha=0.1).fit(X_train,y_train)

print("alpha=0.1")
print("訓練データへの決定係数　：{:.3f}" .format(reg.score(X_train, y_train)))
print("テストデータへの決定係数：{:.3f}" .format(reg.score(X_test, y_test)))

reg = linear_model.Ridge(alpha=0.5).fit(X_train,y_train)

print("alpha=0.5")
print("訓練データへの決定係数　：{:.3f}" .format(reg.score(X_train, y_train)))
print("テストデータへの決定係数：{:.3f}" .format(reg.score(X_test, y_test)))

reg = linear_model.Ridge(alpha=1).fit(X_train,y_train)

print("alpha=1")
print("訓練データへの決定係数　：{:.3f}" .format(reg.score(X_train, y_train)))
print("テストデータへの決定係数：{:.3f}" .format(reg.score(X_test, y_test)))

こんな結果になりました。

alpha=0
訓練データへの決定係数　：0.737
テストデータへの決定係数：0.746
alpha=0.1
訓練データへの決定係数　：0.737
テストデータへの決定係数：0.745
alpha=0.5
訓練データへの決定係数　：0.736
テストデータへの決定係数：0.741
alpha=1
訓練データへの決定係数　：0.735
テストデータへの決定係数：0.738

alphaが0に近いほど、「訓練データのほうが精度（決定係数）が高く、テストデータへの精度が低い」となってくれるとリッジ回帰の効果があった、と言えたのですが・・・どうやらボストン住宅価格データに対しては通常の最小二乗法でも行けそうな感じの結果となりました・・・

ちなみに、alphaを0とすると、通常の最小二乗法による回帰になります。↓が最小二乗法による回帰の結果です。

#通常の最小二乗法による線形回帰
reg2 = linear_model.LinearRegression().fit(X_train,y_train)

print("訓練データへの決定係数　：{:.3f}" .format(reg2.score(X_train, y_train)))
print("テストデータへの決定係数：{:.3f}" .format(reg2.score(X_test, y_test)))

訓練データへの決定係数　：0.737
テストデータへの決定係数：0.746

まとめ：機械学習の回帰では基本的にリッジ

scikit-learnの「こんな時にはこのアルゴリズム使ったらいいよ的な図」には、通常の最小二乗法による回帰は入っていないので、基本的に、リッジ回帰が包括的に使えるという感覚で良いとおもいました。alphaを0にすると最小二乗法と同じになりますし。