ロジスティック回帰などは線形モデルということで、線形モデルが何かを勉強してみました。
機械学習アルゴリズムの基本だね。
教師あり学習の分類ができる機械学習アルゴリズムで、ロジスティック回帰というものを何回か利用してきました。ロジスティック回帰の中身が知りたい、と思い勉強していたのですが、まずは線形モデル、というものを理解しなければ何も始まらないことがわかりました。
こんな人の役に立つかも
・機械学習プログラミングを勉強している人
・線形モデルとは何かを理解したい人
・機械学習の分類における線形モデルについて知りたい人
分類を行う線形モデル
線形モデルは、
(w0 × X0) + (w1 × X1) + … + (wn + Xn) + b= 0
という式で「境界を表現」します。nの値は特徴量の数です。2次元(2特徴量)のデータであれば直線を示し、3次元であれば、平面を表現します。たしか、4次元以上は超平面といっていたはず・・・
いきなり数式!?これだとイメージしづらいな・・・
2次元の場合を考えてみました。
以前、可視化しやすいようにアヤメのデータを2次元化しました。2次元化されたデータ(特徴量が2つのデータ)を例に、線形モデルがどのように動作しているかを見てみました。

2次元の場合の線形モデル
2次元のアヤメデータの場合、特徴量が2つなので、機械学習アルゴリズム(例えばロジスティック回帰)は次の式で、境界「線」を作ろうとします。
(w0 × X0) + (w1 × X1) + b = 0
2次元なので、w1までの式となります。
このときに、w0とw1、bの値を訓練データからちょうどよい部分を見つける、という動作が「fit」で行われる訓練になってきます。
プログラムで境界線を検証
まずは、importから境界線を描く関数を定義します。
#ロジスティック回帰
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
import numpy as np
import matplotlib.pyplot as plt
panda_box = load_iris()
X = panda_box.data
y = panda_box.target
X_2dim = panda_box.data[:,:2]
#関数を作成
def make_meshgrid(x, y, h=.02):
x_min, x_max = x.min() - 1, x.max() + 1
y_min, y_max = y.min() - 1, y.max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
return xx, yy
def plot_contours(ax, clf, xx, yy, **params):
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx, yy, Z, **params)
return out
def graf_setting(ax):
#ax.set_xticks(())
#ax.set_yticks(())
ax.set_xlabel('Sepal length')
ax.set_ylabel('Sepal width')
#2クラス(「setosa」と「versinica」のみ)のデータを作成
X_2dim_2cls = X_2dim[y!=2]
y_2cls = y[y!=2]次に、ロジスティック回帰に訓練データを訓練させます。今回はデータ全部投入です。
訓練ができると、先ほどの
(w0 × X0) + (w1 × X1) + b = 0
のw0とw1とbが算出されます。
#2クラス
#===ロジスティック回帰の作成===
#訓練
clf = LogisticRegression().fit(X_2dim_2cls, y_2cls)
#w0 W1の値
print(clf.coef_)
#bの値
print(clf.intercept_)w0とw1は「coef_」に、また、bの値は「intercept_」に入っていますので、表示してみます。
[[ 3.0786959 -3.0220097]]
[-7.30634549]ロジスティック回帰の境界線は
(3.0786959 × X0) + (-3.0220097 × X1) – 7.30634549 = 0
という式が算出されました。
X0は「sepal length」の軸で、X1が「sepal width」の軸に対応します。
最後に境界線を視覚化しておきます。
#空のグラフを作成
fig = plt.figure(figsize=(9, 4))
ax = fig.add_subplot(121)
#グリッドのデータを作成
X0, X1 = X_2dim_2cls[:, 0], X_2dim_2cls[:, 1]
xx, yy = make_meshgrid(X0, X1)
#グラフに境界線とデータをプロット
plot_contours(ax, clf, xx, yy, cmap=plt.cm.coolwarm, alpha=0.8)
ax.scatter(X0, X1, c=y_2cls, cmap=plt.cm.coolwarm, s=20, edgecolors='k')
graf_setting(ax)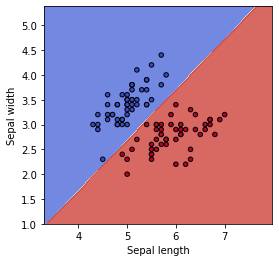
実際に、2次元の境界線の式として
(3.0786959 × X0) + (-3.0220097 × X1) – 7.30634549 = 0
だと算数が苦手な私には直感的ではないので、X1=の形に変更してみます。
「y=ax + b」は、小さいころに習う直線の式ですね^^;
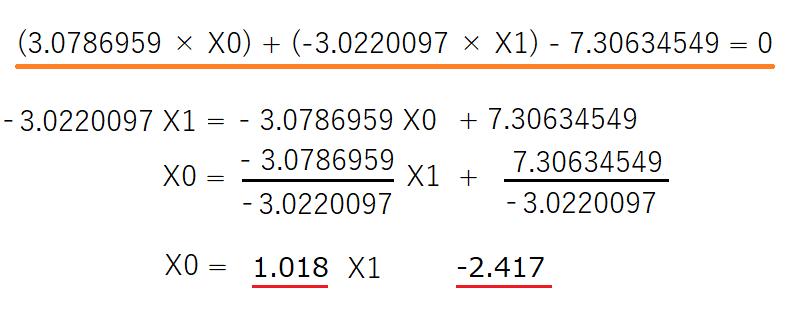
泥臭く計算してみた結果、ロジスティック回帰がsepal lengthとsepal wifdthのデータを分類する境界線はこのような直線になりました。
座標を0まで描くと、こんなイメージになります。
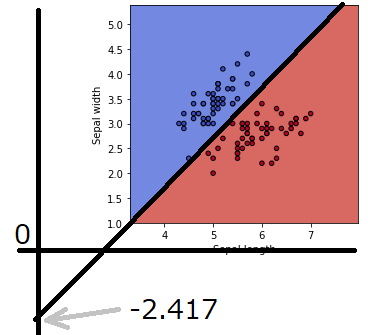
なんとなく、線形モデルの意味合いが身近な気がしてきました。
数式を身近なものに例えられるとなんとなく理解できるよね。

