ルックアップテーブルについて、もう少し深く調べる必要がありそうです。
オシレータにいろいろな波形を自作できると、世界が広がりそうだね~
JUCEチュートリアル、Introduction to DSPの「Changing the oscillator waveform」の項目を進めていきたいと思います。以前のオシレータの実装で、少し疑問に感じた部分などの検証を入れつつ進めていきます。
公式のチュートリアルはこちらです。
こんな人の役に立つかも
・JUCEのオシレータクラスでいろいろな波形を作成したい人
・JUCEのoscillatorクラスのinitialise関数の挙動について調べている人
・JUCEチュートリアルのIntoroduction to DSPをやっている人
Oscillatorクラスのinitialize関数
juce::Oscillatorクラスのinitializeの挙動について探っていこうと思います。Type xと、ラムダ式に渡されるものがどのような数値かを確認します。
まず、ラムダ式のxの引数について、どのような値が入ってくるかを見てみました。
osc.initialise([](Type x)
{
DBG("val:" << x);
return std::sin(x);
}, 128);初期時に、次のように-3.14~3.14までの値(-PI~PI)の値が渡されてきていました。
val:-3.14159
val:-3.09212
val:-3.04264
...省略...
val:3.09212
val:3.14159Pythonで、xが-3.14…~3.14…の値を取るときのsinをグラフ化してみました。(Pythonプログラムをgoogle Colaboratoryで実行しました。)
input_xというリストに、xのとる128段階の-PI~PIの値を格納しました。(デバッグの数値をコピペしました。)
#これはPython
import matplotlib.pyplot as plt
import math
input_x = [-3.14159,-3.09212,-3.04264,-2.99317,-2.9437,-2.89422,-2.84475,-2.79528,-2.7458,-2.69633,-2.64685,-2.59738,-2.54791,-2.49843,-2.44896,-2.39948,-2.35001,-2.30054,-2.25106,-2.20159,-2.15211,-2.10264,-2.05317,-2.00369,-1.95422,-1.90475,-1.85527,-1.8058,-1.75632,-1.70685,-1.65738,-1.6079,-1.55843,-1.50895,-1.45948,-1.41001,-1.36053,-1.31106,-1.26158,-1.21211,-1.16264,-1.11316,-1.06369,-1.01421,-0.964741,-0.915267,-0.865793,-0.816319,-0.766845,-0.717371,-0.667898,-0.618424,-0.56895,-0.519476,-0.470002,-0.420528,-0.371054,-0.32158,-0.272107,-0.222633,-0.173159,-0.123685,-0.0742109,-0.0247369,0.0247369,0.0742106,0.123685,0.173159,0.222633,0.272106,0.32158,0.371054,0.420528,0.470002,0.519476,0.56895,0.618424,0.667897,0.717372,0.766845,0.816319,0.865793,0.915267,0.964741,1.01422,1.06369,1.11316,1.16264,1.21211,1.26158,1.31106,1.36053,1.41001,1.45948,1.50895,1.55843,1.6079,1.65738,1.70685,1.75632,1.8058,1.85527,1.90475,1.95422,2.00369,2.05317,2.10264,2.15211,2.20159,2.25106,2.30054,2.35001,2.39948,2.44896,2.49843,2.54791,2.59738,2.64685,2.69633,2.7458,2.79528,2.84475,2.89422,2.9437,2.99317,3.04265,3.09212,3.14159]
sin_list = []
for x in input_x:
sin_list.append(math.sin(x));
plt.plot(sin_list)このinput_xの値の最初の-3.14159から128回sinに与えられると、次のようなsin出力となります。
実際には、128個のルックアップテーブルの要素に-1.0~1.0の値が入っているようなデータになります。
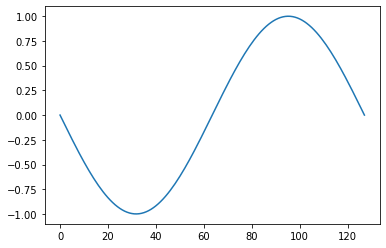
このことから、dsp::oscillatorクラスのinitialize関数のラムダ式で入力されるxの値は、ルックアップテーブルのサンプル数分、-PI~PIの値を等間隔に増加するような値ということがわかります。
Xは、時間方向の数値ですね。
-180度~180度の範囲の波形というイメージだね~
のこぎり波の実装
オシレータのinitialise関数のラムダ式を以下のように変更するだけです。
osc.initialise([](Type x)
{
return juce::jmap(x,
Type(-juce::MathConstants<double>::pi),
Type(juce::MathConstants<double>::pi),
Type(-1),
Type(1));
}, 2);次のようなのこぎり波が出力されるようになります。
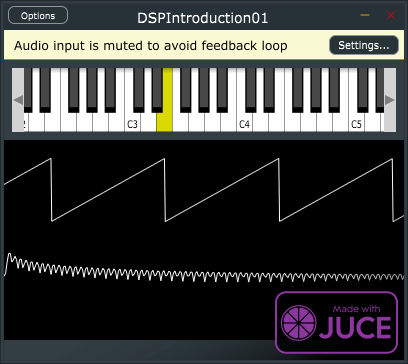
今回ルックアップテーブルのサンプル数が2だけとなっています。これは、のこぎり波は、2つの点があれば成り立つので、このようになっているようです。
このとき、xには、-3.14159と3.14159の2つが入ってきます。
jmap関数は、第二引数~第三引数の範囲の値を第四引数~第五引数の範囲の値にマッピングしてくれます。第一引数に変換する値を入れるので、今回は、xが-3.14159のときは、-1、xが3.14159のときは1という値になり、[-1.0,1.0]というようなデータ数2のルックアップテーブルになります。
ルックアップテーブルの間は、直線で補間されているので、線形補間というやつでしょうか。
三角波にチャレンジ
※ここからは、チュートリアルのチャレンジの項目となりますので、自分で挑戦したい方は見ないほうが良いと思います。
三角波にチャレンジしてみました。三角波はsin波形を重ね合わせて作成することもできますが、ルックアップテーブルの点を指定することでも作成することができますので、のこぎり波と同じような考えで作成してみました。
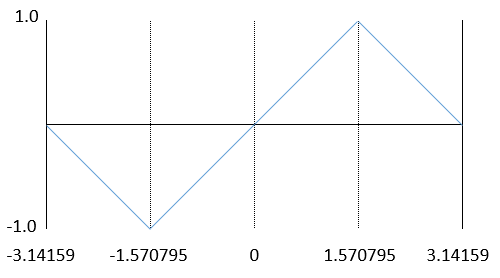
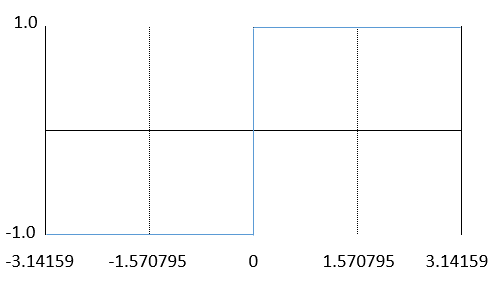
ルックアップテーブルには5つのポイントを登録すれば三角波になりますので、上の図のようにxの値がそれぞれ-3.14159、-1.570795…のときにそれぞれ0.0、-1.0…というゲイン値をとればいいことがわかります。そこで、次のようなプログラムを作成してみました。
osc.initialise([](Type x)
{
if (x < -3.14) {
return 0.0;
}
else if (x >= -3.14 && x < -1.57){
return -1.0;
}
else if (x >= -1.57 && x < 1.57) {
return 0.0;
}
else if (x >= 1.57 && x < 3.14) {
return 1.0;
}
else {
return 0.0;
}
}, 5);男の条件分岐です。
ダイレクトすぎるよね・・・
returnがたくさん出てくるなど、泥臭くなっていますが、とりあえず、実行したところ、つぎのような出力が得れらえました。
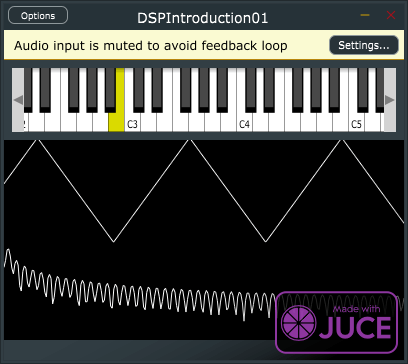
ルックアップテーブルを利用した波形の作成では、sin波を重ね合わせるような作成をしなくても、絵を描くようにいろいろな波形が生成できそうです。
矩形波にチャレンジ
次に、矩形波を作成していきたいと思います。
矩形波は、xが0のときに一気に-1から1に値が変化するような波形ですが、実際には、あるxの値で-1、その次のxの値で1というように、完全な垂直の線とすることは不可能です。そのため、ルックアップテーブルの分解能を上げると、限りなく垂直の線に近づいていきます。
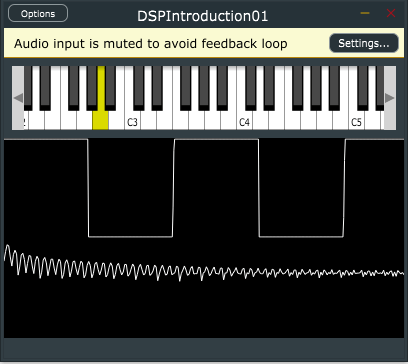
とりあえず、サイン波では128サンプルでしたので、同じ設定でやってみました。
プログラムは次のようにしました。
osc.initialise([](Type x)
{
if (x < 0) {
return -1.0;
}
else {
return 1.0;
}
}, 128);単純に0より小さなXのときは-1、0以上のときは1を出力します。
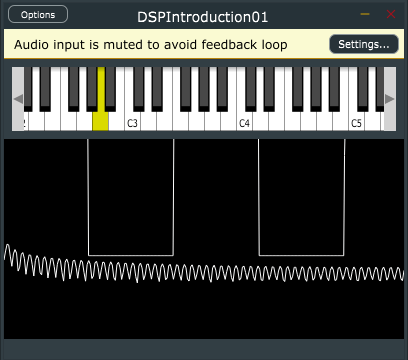
若干、垂直ではないので、もう少しサンプル数を多くすることで理想的な矩形波に近づけることもできそうです。
256のデータ数にしたら次のようになりました。(同じA2の音です)
ちなみに、64のデータ数とすると次のようになりました。
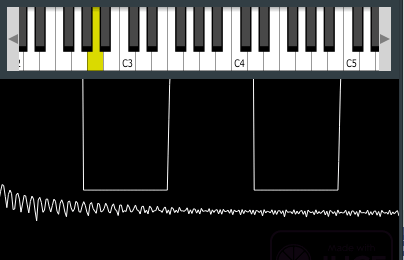
目視では、若干ですが、波形の変動する部分が緩やかになってきています。
DSPやってる感がでてきました。

