JUCEプログラミング、Visualise the frequencies of a signal in real time3、周波数表示のデモアプリ作成２

引き続き、JUCEチュートリアルの「DSP」の項目、「Visualise the frequencies of a signal in real time」を進めていきます。前回に続き、スペクトルアナライザのアプリを実装していきます。今回は描画に関する関数を実装していきます。スケーリングに関する部分は、Pythonのmatplotlibでグラフ化してみました。

前回の記事もご参照ください。

公式チュートリアルはこちらになります。

https://docs.juce.com/master/tutorial_spectrum_analyser.html

こんな人の役に立つかも

・JUCEチュートリアル「Visualise the frequencies of a signal in real time」をやっている人

・JUCEでスペクトルアナライザを実装したい人

paint関数

paint関数を以下のように変更しました。

画面の描画領域を描く関数です。今回は、TimerCallback関数で１秒間に３０回呼び出されます。

void MainComponent::paint (juce::Graphics& g)
{
    g.fillAll(juce::Colours::black);

    g.setOpacity(1.0f);
    g.setColour(juce::Colours::white);
    drawFrame(g);
}

fillAllで全体を黒色に塗りつぶし、setOpacity関数でこの後にgで描画する際の透明度の設定を完全に不透明にしています。

「g.setColour」関数で描画色を白に設定します。

そして、周波数の描画を行う「drawFrame」関数にgraphicsクラスのオブジェクトであるgを渡しています。drawFrameはこの後に実装します。

drawFrame関数

次のdrawFrame関数をMainComponent.cppファイルに追記します。

MainComponent.cppファイルの最後に以下のdrawFrame関数を追記しました。

void MainComponent::drawFrame(juce::Graphics& g)
{
    for (int i = 1; i < scopeSize; ++i)
    {
        auto width = getLocalBounds().getWidth();
        auto height = getLocalBounds().getHeight();

        //スペクトルの線分を引きます。
        g.drawLine({ (float)juce::jmap(i - 1, 0, scopeSize - 1, 0, width),
                            juce::jmap(scopeData[i - 1], 0.0f, 1.0f, (float)height, 0.0f),
                     (float)juce::jmap(i,     0, scopeSize - 1, 0, width),
                            juce::jmap(scopeData[i],     0.0f, 1.0f, (float)height, 0.0f) });
    }
}

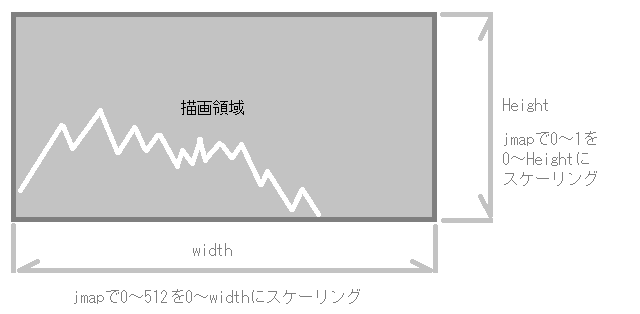
scopeSize回数分drawLineで線を引きます。scopeSizeは今回512という数値にしましたので、512回線分を引く処理を繰り返します。

drawLine関数は第一引数、第二引数で始点座標、第三引数、第四引数で終点座標を指定します。

また、jmap関数は、「第二引数～第三引数」の範囲の第一引数の数値を、「第四引数～第五引数」の範囲にスケーリングしなおす関数です。

そして、scopeData配列には、この後に実装するdrawNextFrameOfSpectrum関数で、各周波数ポイントの「振幅スペクトル」のデータが格納されています。

これらの関数とデータを利用して、drawLine関数の引数に与えることでスペクトルを描画します。drawLineの始点として、（i-1，scopeData[i-1]）とすることで、一つ前の周波数の線分の終点位置となります。そして、現在の周波数（横軸）の座標を終点位置として（i，scopeData[i]）とすることで、前の周波数の位置から現在の周波数の位置まで線分を引くことができます。

TimerCallback関数

TimerCallback関数もMainComponent.cppに追記します。

コンストラクタのstartTimerHz関数で1秒間に30回呼び出される設定をしたTimerCallback関数です。

void MainComponent::timerCallback()
{
    if (nextFFTBlockReady)
    {
        drawNextFrameOfSpectrum();
        nextFFTBlockReady = false;
        repaint();
    }
}

nextFFTBlockReadyフラグがTrueのとき、この後に実装するdrawNextFrameOfSpectrum関数を呼び出します。そして、nextFFTBlockReadyフラグをfalseに設定してrepaint関数でpaint関数の処理を呼び出します。

nextFFTBlockReadyフラグがTrueということは、fftDataにデータ格納が完了しているということなので、fftDataにデータが準備できたら処理を行うという意味になります。また、drawNextFrameOfSpectrum関数でfftDataを利用し終わったら、nextFFTBlockReadyフラグをfalseにすることで、音声処理スレッドのfftDataへのデータ格納が再度始まるようになります。音声処理スレッドの実装は前回の記事を参考ください。

drawNextFrameOfSpectrum関数

MainComponent.cppに追記します。

drawNextFrameOfSpectrum関数は、scopeData配列を作成するための関数です。FFTを行って振幅スペクトルに変換した後、scopeData配列に512点の周波数ポイントのデシベル値を格納します。

void MainComponent::drawNextFrameOfSpectrum()
{
    //[1]窓関数を適用します。
    window.multiplyWithWindowingTable(fftData, fftSize);

    //[2]FFTで振幅スペクトルに変換します。
    forwardFFT.performFrequencyOnlyForwardTransform(fftData);

    auto mindB = -100.0f;
    auto maxdB = 0.0f;

    //[3]512回繰り返して周波数表示用の配列scopeDataを作成します。
    for (int i = 0; i < scopeSize; ++i)
    {
        //[3-1]取得する周波数のポイントをスケーリングして、fftData配列のインデックス番号を計算します。
        auto skewedProportionX = 1.0f - std::exp(std::log(1.0f - (float)i / (float)scopeSize) * 0.2f);
        auto fftDataIndex = juce::jlimit(0, fftSize / 2, (int)(skewedProportionX * (float)fftSize * 0.5f));
        //[3-2]周波数ポイントの振幅0~1をデシベルに変換してlevelとします。
        auto level = juce::jmap(juce::jlimit(mindB, maxdB, juce::Decibels::gainToDecibels(fftData[fftDataIndex])
            - juce::Decibels::gainToDecibels((float)fftSize)),
            mindB, maxdB, 0.0f, 1.0f);

        scopeData[i] = level;
    }
}

[1]で、窓関数を適用します。今回は「ハン窓」をコンストラクタで指定しました。これで、2048ポイントの時系列の音声データの最初と最後がフェードインフェードアウトみたいになります。

[2]で、FFT処理で振幅スペクトルを取得します。今回得られる振幅スペクトルは、fftDataが4096個の配列で、その半分の2048個にサンプリングレート44100Hzまでの振幅が格納されます。ナイキスト周波数が有効な周波数の半分となるため、配列の最初から1024個が使うことのできる周波数データとなります。

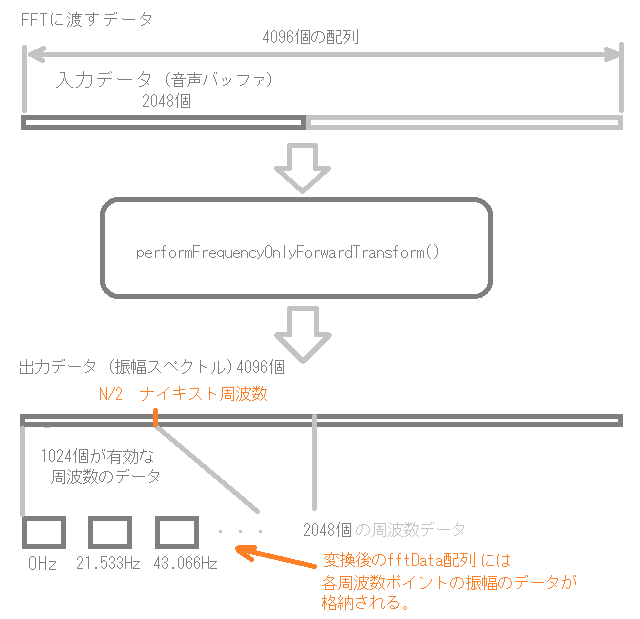
fftData配列には、先頭から1024個までに、↑のよう2048個目がサンプリングレート44.1kHzとなる周波数ポイントの振幅のデータ（ゲイン）が入ります。今回の場合、周波数のポイントは約20Hz刻みとなります。

[3]で、この約20Hz刻みのデータから、512個の表示用のscopeData配列を作成します。スペクトルは、表示するとき高周波ほど細かいスケーリングとなるので、右に行くほど（高周波の方）小さな間隔で大きく周波数が増加するように表示します。

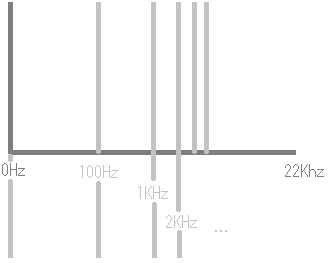
skewedProportionXとして、0~512までの増加を、0~1までの次のような変化として取得できます。

google Colaboratoryにて、「skewedProportionX」の計算をPythonで行ってみると、次のようになります。

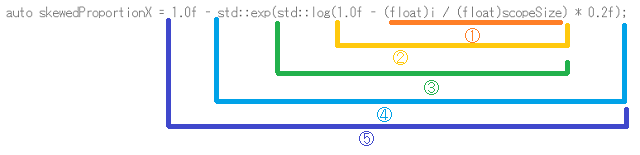
#① i / 512
import matplotlib.pyplot as plt
import math

list = []

for num in range(1,512):
  list.append(num/512)

plt.plot(list)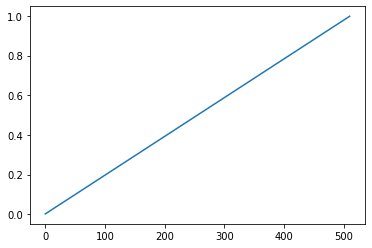

#②　1.0f - ( i / 512 )
list2 = []
for x in list:
  list2.append(1 - x)

plt.plot(list2)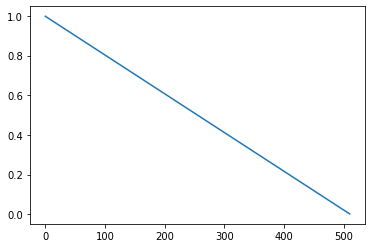

#③　log( 1.0f - (i / 512))
list3 = []

for x in list2:
    list3.append(math.log(x))

plt.plot(list3)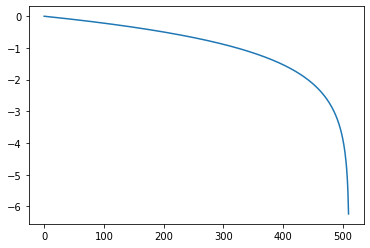

#④　EXP(log)
list4 = []
for x in list3:
  list4.append(math.exp(x * 0.2))

plt.plot(list4)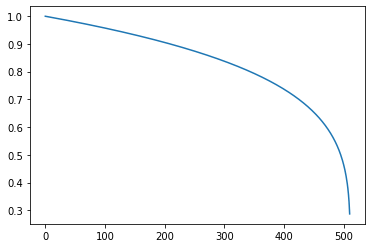

#⑤　1-EXP（skewedPropotionX）
list5 = []
for x in list4:
  list5.append(1 - x)

plt.plot(list5)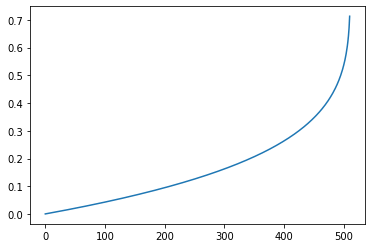

skewedPropotionX変数は、iが0から512へと変化するにつれて0~1の間で↑のグラフのように変化していきます。これを1024（fftSize/2）の数値に掛け合わせることで、fftDataのインデックス番号とします。

最後に、[3-2]では、先ほど得られたインデックス番号をfftDataのインデックス番号に入れることで、高周波にいくほど周波数の増加量が多くなるような周波数データの参照ができることになります。そして、gainToDecibels関数で、scopeDataにデシベルとして振幅データを変換して格納します。jlim関数で、上限と下限は-100db～0dbと制限をかけています。