ウェーブテーブル方式について、プログラムを元に、もう少し詳細に考察をしてみました。
図にできるとわかりやすいよね〜
JUCEでウェーブテーブルのオシレータを実装しましたが、仕組み的に何となくイメージは出来るのですが、具体的にどのようになっているのか、図化しながら考察をしてみました。今回は、公式チュートリアルにはない内容となりますので、ご了承ください。
こんな人の役に立つかも
・JUCEでプログラミングの勉強をしている人
・JUCEチュートリアル「Wavetable synthesis」を勉強している人
・ウェーブテーブルの仕組みを勉強している人
ウェーブテーブルについて
例えば、128サンプルのウェーブテーブルにサイン波を格納するような場合を考えると、作成されるテーブルは次のようなものになります。今回のプログラムでは、このテーブルの作成をcreateWavetableでプログラムの最初に一回行います。
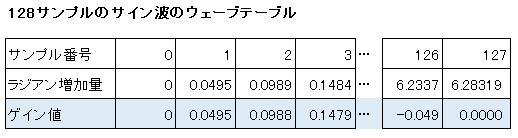
テーブルには128サンプルしかないので、サイン波1周期分を128サンプルに収めようとすると、1サンプル毎で、{(2×π)÷(128-1)}ラジアン毎のサインの数値を格納していくことになります。
128-1としているのは、例えばサンプル数が2のときは、0⇒128となるので、増加する回数は1回になるように、128サンプルだと増加する回数が127と1回少なくなるので、ラジアン360度(6.28319)を127で割ることで1サンプル当たりのラジアン増加量とします。
その結果、上の表の青色の列のような値が0~127(計128サンプル)となります。
再度確認すると、createWavetable関数のサイン波をウェーブテーブルに格納する処理は次のようになっています。
//createWavetable関数でのサンプル当たりのラジアンを求める処理です。
auto angleDelta = juce::MathConstants<double>::twoPi / (double)(tableSize - 1);
//ウェーブテーブルのサンプル数分ループです。
for (unsigned int i = 0; i < tableSize; ++i)
{
//ラジアンでサンプルに格納するサイン波のゲインを求めます。
auto sample = std::sin(currentAngle);
//ウェーブテーブルのサンプルにゲイン値をfloatで格納します。
samples[i] = (float)sample;
//ラジアンを次のサンプルのために進めます。
currentAngle += angleDelta;
}このような処理で青色の列のようにウェーブテーブルの各サンプルに値が保存されます。
この値は、サイン波の縦軸のゲイン値になりますので、このポイントをつなぐと、次のように1周期当たりの分解能が128のサイン波となります。
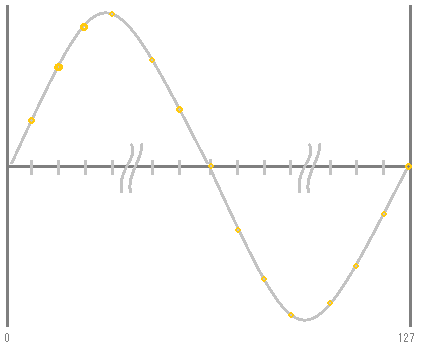
ウェーブテーブルは、このように一定の分解能のサンプル数で波形をあらかじめ保持しておくようなものになります。
ウェーブテーブルって、結局サンプル間のところは補完するから、完全なサイン波になるというわけではないのですね。
補完のアルゴリズム考えるだけでもいろいろとオシレータに個性が出そう
WavetableOscillatorクラス
Wavetableクラスの重要な関数、「setFrequency」と「getNextSamples」を見ていきたいと思います。
setFrequency関数
void setFrequency (float frequency, float sampleRate)
{
auto tableSizeOverSampleRate = (float) wavetable.getNumSamples() / sampleRate;
tableDelta = frequency * tableSizeOverSampleRate;
}setFrequencyで求めるべき値は、「tableDelta」です。これは、時間的基準がない128のサンプルということができますので、外部から時間的基準をあたえることで、1サンプル当たりの時間は変化するようなテーブルになります。
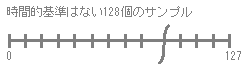
サンプルレート44100の2Hzのサイン波を128サンプルのウェーブテーブルから再生したい場合のtableDeltaを例に考えてみます。
サンプルレート44100に対する2Hzの周波数は、次のように22050サンプル数で1周期とすればよいことがわかります。

44100÷2Hz = 22050
tableDeltaは先のように128サンプルで1周期のサイン波を表現しているので、22050サンプルで1周期を表現するような128を100%とする増加量は、
128÷22050 ≒ 0.0058…
となります。
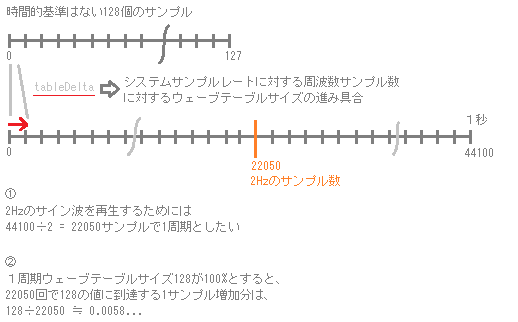
この計算をまとめると、
BufferSize ÷(SampleRate/Hz)となります。
この式を変形すると
BufferSize × (Hz/SampleRate) = BufferSize/SampleRate × Hz
となるので、プログラムの2行の計算式となります。
音声処理は式変形ないと理解しづらいものが多いですね・・・
getNextSample関数
getNextSample関数は、ウェーブテーブルのサンプルとサンプルの間を補完するような処理です。
forcedinline float getNextSample() noexcept
{
auto tableSize = (unsigned int) wavetable.getNumSamples();
auto index0 = (unsigned int) currentIndex;
auto index1 = index0 == (tableSize - 1) ? (unsigned int) 0 : index0 + 1;
auto frac = currentIndex - (float) index0;
auto* table = wavetable.getReadPointer (0);
auto value0 = table[index0];
auto value1 = table[index1];
//補完の式です。
auto currentSample = value0 + frac * (value1 - value0);
if ((currentIndex += tableDelta) > (float) tableSize)
currentIndex -= (float) tableSize;
return currentSample;
}index0変数とindex1変数は整数、で取得して、currentIndexは小数である点がポイントです。index0とindex1は、ウェーブテーブルの0~128のサンプル数で、currentIndexのポイントを挟むように移動していきます。
キャストによって、小数部分はきりすてられますので、index0は、currentIndexを挟む小さいほうの整数になることとなります。

index1は、index0の次のサンプル数を示します。(index1はウェーブテーブルサンプル数を越えると0に戻ります。)
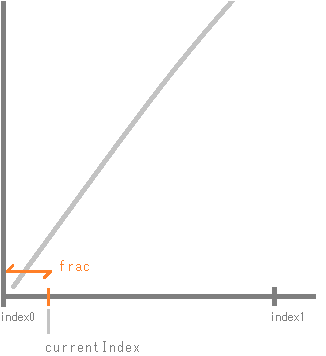
この関数内で一番重要な式が、補完の式です。
value0 + frac * (value1 – value0)
value0とvalue1は、currentIndexを挟む2サンプルのゲイン値として先に取得していますので、この2ゲイン値を引いて、fracを掛け合わせると、index0~index1の間のゲイン増加量が計算できます。それにindex0のゲイン値を足すことで、ウェーブテーブルのサンプルとサンプルの間を補完するような計算としています。
補完、といっても、サンプルとサンプルの間はかけ算なので、線形な増加になるんですね~
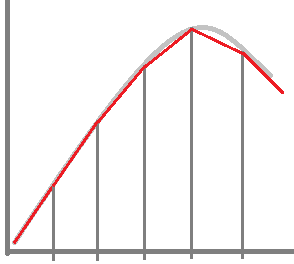
ウェーブテーブルのサンプル数が少ないと、サイン波の頂点あたりの補完が怪しそうですね~、実際のところはどうなんでしょうか。
いろいろなソフトシンセを使っていても、同じサイン波で雰囲気が違うように感じられるので、実際には、補完のアルゴリズムなどで、サイン波一つとってもいろいろな音の違いというものはありそうな気がしてきました。
微妙な違いだけれど、いろいろと工夫は出来そう・・・

